Prednáška "Evolučné algoritmy"
MFF UK, 4. ročník, odbor "informatika"
Šk.r. 1999/00, semester zimný
Dátum prednášky:
útorok o 11.30 hod, poslucháreň IV
Sylabus prednášky:
Prednášajúci: Prof. V. Kvasnička a Doc. J. Pospíchal {kvasnic@cvt.stuba.sk}
Katedra matematiky CHTF STU,
Semester: zimný
Rozsah: 2-0-0
Literatúra:
Charles Darwin "On the Origin of Species" (
doc)
Úvodná kapitola z knihy "
Evolutionary Design by Computers", editor Peter J. BentleyISBN 1-55860-605-X, domovská stránka knihy je na adrese
http://www.mkp.com/books_catalog/1-55860-605-x.asp
text kapitoly
pdf.
Tutoriál od Prof.
Hans-Paul Schwefel "On Natural Life's Tricks to Survive and Evolve"
Pripravovaná kniha "Evolučné
algoritmy"Jednotlivé kapitoly môžu slúžiť ako základný text prednášky, kde sú uvedené aj príklady na precvičenie.
Obsah
Kapitola 1- Úvodné poznámky (
ps.zip alebo pdf)Kapitola 2 - Základné pojmy evolučných algoritmov (
ps.zip alebo pdf)Kapitola 3 - Horolezecké algoritmy (
ps.zip alebo pdf)Kapitola 4 - Genetické algoritmy (
ps.zip alebo pdf)Kapitola 5 - Genetické programovanie (
ps.zip alebo pdf)Kapitola 6 - Simulované žíhanie (
ps.zip alebo pdf)Kapitola 7 - Kombinatoriálne optimalizačné problémy (
ps.zip alebo pdf)Kapitola 8 - Evolučné stratégie (
ps.zip alebo pdf)Kapitola 9 - Umelý život (
ps.zip alebo pdf)Kapitola 10 - Neurónové siete (
ps.zip alebo pdf)
1. prednáška (28. 9. 1999)
Všeobecné predstavy o darvinovskej evolúcii, chápanie evolúcie ako algoritmu, význam učenia v evolúcii (Baldwinov efekt), mémy (Dawkins) ako nosič informácie pre chromozómy.
Priesvitky k prednáške (ps.zip alebo pdf)
Pozri tiež pripravovaný článok "Umelá evolúcia" (
ps.zip alebo pdf)
2. prednáška (5. 10. 1999)
Binárne kódovanie reálnej premenne, transformácia spojitého optimalizačného problému na binárny optimalizačný problém. Slepý algoritmus, horolezecký algoritmus (hill climbing), horolezecký algoritmus a učením, metóda zakázaného prehľadávania (tabo search), evolučné programovanie. Predmet tejto prednášky odpovedá 2. a 3. kapitole knihy "Evolučné algoritmy".
Priesvitky k prednáške (ps.zip alebo pdf)
3. prednáška (12. 10. 1999)
Genetické algoritmy, "messy" genetický algoritmus, paralélny genetický algoritmus. Základné princípy genetických algoritmov.
Priesvitky k prednáške (ps.zip alebo pdf)
4. prednáška (19. 10. 1999)
Teória genetických algoritmov.
Priesvitky k prednáške (ps.zip alebo pdf)
5. prednáška (26. 10. 1999)
Genetické programovanie, symbolická regresia.
Priesvitky k prednáške (ps.zip alebo pdf)
6. prednáška (2. 11. 1999)
Simulované žíhanie.
Priesvitky k prednáške (ps.zip alebo pdf)
7. prednáška (9. 11. 1999)
Kombinatoriálne optimalizačné problémy. Úloha obchodného cestujúceho, Number Partitioning Problem.
Priesvitky k prednáške (ps.zip alebo pdf)
8. prednáška (16. 11. 1999)
Evolučné stratégie.
Priesvitky k prednáške (ps.zip alebo pdf)
9. prednáška (23. 11. 1999)
Umelý život.
Priesvitky k prednáške (ps.zip alebo pdf)
10. prednáška (30. 11. 1999)
Neurónové siete.
Priesvitky k prednáške (ps.zip alebo pdf)
11. prednáška (7. 12. 1999)
Podrobnosti o skúške, témy "case studies" (ps.zip alebo pdf)
Skúška - témy "case studies"
Skúška z prednášky "Evolučné algoritmy" bude udelená na základe vypracovanej "case study" z oblastí uvedených nižšie. "Case study" je písomná práca v rozsahu približne 7-10 strán (page size A4, font size 10, line spacing single, obsahuje meno autora a jeho internetovské koordináty), obsahuje teoretický popis použitej metódy a získané numerické výsledky, kt
oré sú ilustrované tabuľkami a grafmi. Integrálnou prílohou "case study" bude aj fungujúci program, pomocou ktorého bola vypracovaná jej aplikačná časť.Skúška sa uskutoční na Katedre matematiky CHTF STU vždy v piatok v intervale od 9-11 hod., na skúšku je potrebné sa prihlásiť na t.č. 59325296 alebo emailom {kvasnic,pospich}@cvt.stuba.sk
Každá téma z "case study" bude mocť byť použitá iba jedným študentom, na tému sa treba prihlásiť a postupné "prideľovanie" bude prebiehať podľa pravidla “kto skôr príde..”. Podstatou skúšky bude diskusia o riešenej úlohe a taktiež všeobecné vedomosti z evolučných algoritmov.
Upozornenie: Záujemci o skúšku FTP uploadujú aspoň jeden deň pred konaním skúšky (do 16.00 hod.) vypracovanú "case study" na adresu
ftp://math.chtf.stuba.sk/received/vlado
v PS alebo v PDF formáte, pričom "čitateľnosť" súborov nech je prekontrolovaná pomocou GhostView-u alebo AcrobatReader-u. Práce budú vystavené na tejto stránke pre poučenie budúcich generácií.
Ako vytvoriť PS dokument pomocou M
S WORD-u: Priradí sa poscriptovská tlačiareň a nechá sa tlačiť do súboru (print to file), takto vznikne PS súbor, je potrebné ho ešte prekontrolovať pomocou GhostView, či sa vytvoril korektne.
Téma 1
. Horolezecký algoritmus pre funkciu f(x) definovanú v![]()
pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokúste sa optimalizovať parametre c0 a Pmut tak, aby ste skoro so 100% istotou dostali globálne minimum s čo najmenším počtom iteračných krokov.
(tému vypracuje V. Škopek)
Téma 2
. Metóda zakázaného hľadania aplikovaná na TSP (riešenie obchodného cestujúceho), pričom cesta nech je vyjadrená pomocou permutácie. Transformačné operátory tÎ S sú realizované ako permutácie transpozícií dvoch objektov. Operátor tij pôsobí na permutáciu P ako transpozícia objektov i a j,![]()
pre i<j. Ako testovací príklad použite ortogonálnu mriežku bodov - miest, kde sa vzdialenosť počíta pomocou Hammingovej metriky (pozri príklad 8.2). Pokúste sa o optimalizáciu veľkosti "s" zakázaného zoznamu T (tabu listu) a maximálneho počtu iterácií time
max pre rôzne hodnoty N dimenzie ortogonálnej mriežky bodov, N=4,5,...,10, tak , aby ste s 95% pravdepodobnosťou dostali korektný výsledok. Podobné úvahy vykonajte aj pre suboptimálne výsledky, ktoré sa líšia len niekoľko málo jednotiek od optimálneho výsledku.(tému vypracuje P. Sučanský)
Téma 3
. Metóda zakázaného hľadania aplikovaná na úlohu N dám na šachovnici. Hľadá sa také umiestnite N dám na šachovnici N´ N tak, aby v každom riadku, stĺpci a diagonále bola umiestnená práve jedna dáma (t.j. neexistuje kolízne postavenie medzi dámami). Zložitosť riešenia tohto problému silne závisí od zvolenej reprezentácie postavenia dám na šachovnici. Jednoduchá reprezentácia postavenia dám je pomocou permutácie P=(p1, p2, ..., pN). Potom dámy na šachovnici sú umiestnené takto: v 1. stĺpci na p1-tom riadku, v 2. stĺpci na p2-tom riadku, atď. Táto jednoduchá reprezentácia rozmiestnenia dám na šachovnici pomocou permutácií má výhodu v tom, že v každom stĺpci a riadku šachovnice sa nachádza práve jedna dáma. Každej permutácii N objektov priradíme celé nezáporné číslo col(P), ktoré odpovedá počtu diagonálnych kolízií. Riešenie problému je potom taká permutácia P, ktorá má nulový počet kolízií, col(P)=0. Funkcia col(P) je určená vzťahom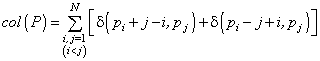
kde d (i,j) je Kroneckerovo delta, d (i,j)=1, pre i=j, d (i,j)=0, pre ią j.
(tému vypracuje P. Droba, skúška dňa 17.12.1999)
Téma 4
. Genetický algoritmus pre funkciu![]()
pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokuste sa nájsť minimálnu veľkosť populácie a také hodnoty pravdepodobností Pcross a Pmut, aby ste skoro so 100% istotou dostali globálne minimum s predpísaným minimálnym počtom krokov.
(tému vypracuje A. Probst, pokus o skúšku dňa 17.12.1999)
Téma 5
. Genetický algoritmus pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke. Použite oba prístupy na kódovanie cesty, tak priamo pomocou permutácie, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.(tému vypracuje M. Zervan)
Téma 6
. Genetický algoritmus pre úlohu Number Partitioning Problem. Použite oba prístupy na kódovanie zobrazenia p , tak priamo pomocou N-tice celých čísel, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.(tému vypracuje P. Imrich)
Téma 7.
Algoritmus simulovaného žíhania pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke. Použite oba prístupy na kódovanie cesty, tak priamo pomocou permutácie, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.(tému vypracuje J. Kľuka, skúška dňa 28.1.2000)
Téma 8
. Evolučná stratégia (1+1). Metódu aplikujete na hľadanie globálneho minima funkcie![]()
pre xÎ [-10,10], ktorá je zovšeobecnená pre viacrozmerný prípad takto
![]()
Použite pravidlo zmeny
s 1/5 úspešnosti a nakreslite graf, kde na vodorovnej osi bude počet generácií a na zvislej aktuálna funkčná hodnota rodiča.(tému vypracuje M. Kubačák, skúška dňa 21.1.2000)
Téma 9
. Genetické programovanie: Implementuje genetický algoritmus (pozri algoritmus 3.5) tak, že chromozómy budú určené ako Readove lineárne kódy s ohodnotením vrcholov podľa (5.18-19). Toto ohodnotenie nech je vykonané tak, že syntaktické stromy budú odpovedať Boolovským funkciám (t.j. funkčné vrcholy sú operácia and, or, xor, a not, a terminálové vrcholy sú jednotlivé Boolovské premenné). Účelová funkcia (5.24) nech je rozšírená o pokutový člen, ktorý bude preferovať syntaktické stromy s menším počtom vrcholov![]()
kde a je malá kladná konštanta a symbol |t| vyjadruje počet vrcholov v strome t. Modifikujete napísanú implementáciu tak že bude odpovedať horolezeckému algoritmu. Porovnajte efektívnosť týchto troch rozdielnych metód pri konštrukcii funkcií, ktoré reprodukujú predpísanú regresnú tabuľku.
(tému vypracuje J. Borovský, skúška dňa 6.4.2000)
Téma 10.
Použitie genetického algoritmu na adaptáciu neurónovej siete. Implementujte neurónovú sieť s dopredným šírením signálu, ktorá obsahuje jednu vrstvu skrytých neurónov a so sigmoidálnou prechodovou funkciou. Použitím genetického algoritmu adaptujte túto neurónovú sieť (t.j. váhy a prahové koeficienty) siete tak, aby s čo najmenšou chybou produkovala rôzne Boolovské funkcie, pričom z numerických dôvodov namiesto hodnoty Boolovských premenných 0 a 1 budeme brať 0.1 a 0.9.(tému vypracuje O. Lonek, skúška dňa 7.1.2000)
Téma 11.
L-systém (tvorba "kríka") je daný nasledovnými pravidlami: (1) štartovný bod F, (2) produkčné pravidlo F ® F [+F][-F], kde F znamená "nakresli čiaru" (začíname kolmou čiarou z počiatočného bodu so súradnicami 0,0 do koncového bodu so súradnicami 0,10). Symbol [ znamená zapamätať si súradnice koncového bodu a zodpovedajúcu zmenu súradnícdx= x koncový - x počiatočný , dy= y koncový - y počiatočný
Symbol ] znamená vrátiť sa na zapamätané súradnice bodu a zodpovedajúce dx a dy, symbol + znamená otočiť sa doľava (použili sme prepis pre súradnice nového bodu
x koncový = x počiatočný + 0.7 (cos(40o) dx - sin(40o) dy)
y koncový = y počiatočný + 0.7 (sin(40
o) dx + cos(40o) dy)Symbol - znamená otočiť sa doprava (použili sme prepis pre súradnice nového bodu
x koncový = x počiatočný + 0.7 (cos(33o) dx + sin(33o) dy)
y koncový = y počiatočný + 0.7 (sin(33
o) dx - cos(33o) dy)Vytvorte obrázok trojrozmerného stromčeka, kde jednotlivé vetvy sa nebudú skracovať faktorom 0.7, ale náhodným číslom s gaussovským rozložením pravdepodobnosti so stredom napr. v 0.7, kde aj hrúbka kmeňa sa bude zmenšovať a bližšie vetvy budú vyzerať hrubšie, kde uhly vetiev v priestore tiež budú dané náhodne. Vyskúšajte aj iné produkčné systémy, napr. počet vetiev bude daný náhodným číslom od 2 d
o 3.(tému vypracuje Š. Baloc)
Téma 12
. Namodelujte priebehy množstva dravcov a koristi ukázané v nasledujúcich obrázkoch podľa rovnícdN1(t)/dt = N1(r1- b1N2 )
dN2(t)/dt = N2(- r2+b2N1
kde N1(t) je počet kusov koristi (alebo hostiteľa) a N2(t) je počet kusov dravcov (alebo parazitov) v čase t. Predpokladáme, že za neprítomnosti dravcov sa korisť rozmnožuje rýchlosťou r1, zatiaľ čo za absencie koristi dravci hynú rýchlosťou r2. Nech b1 zodpovedá schopnosti dravcov požierať korisť a b2 vplyvu množstva koristi (a teda nasýtenia dravcov) na ich rozmnožovanie. Nech r1= 1.5, b1=0.1 r2= 0.25 b2= 0.01 a N1(0)= 15 a N2(0)=20. Znázornite priebeh, nie však pomocou klasického riešenia pomocou diferenciálnych rovníc, ale vytvorením stochastického modelu, kde množstvá dravcov a koristi a ich prírastky/úbytky budú dané celými číslami; v prípade, že zmena nie je vyjadrená celým číslom, berte neceločíselnú časť ako pravdepodobnosť a rozhodnite o zaokrúhlení nahor/nadol na základe porovnania tejto pravdepodobnosti s náhodným číslom z intervalu (0,1) – použite analógiu algoritmov 10.1 a 10.2 z kapitoly o umelom živote. Numericky modelujte a diskutujte pravdepodobnosť zániku jedného či obidvoch druhov v závislosti na počiatočných množstvách jedincov a na ostatných parametroch.
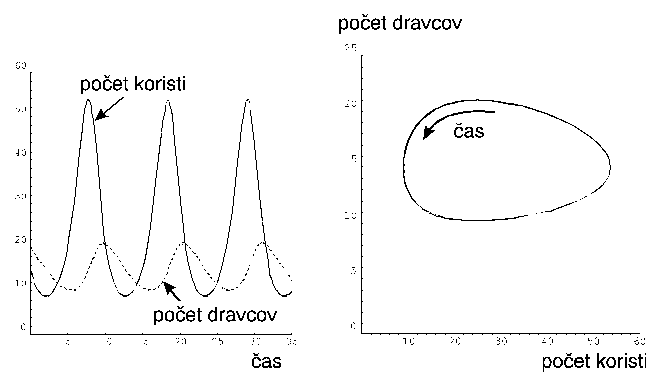
Prvá závislosť ukazuje oscilácie počtu dravcov a množstva koristi v čase, druhý obrázok je trajektóriou sústavy diferenciálnych rovníc (10.4).
(tému vypracuje P. Malčovský)
Téma 13
. Vytvorte program pre animáciu pohybu žubrienok (pozri priložený obrázok), kde veľký kruh je prekážka, "hlavička žubrienok" predstavuje umiestnenie žubrienky v dvojrozmernom priestore a dĺžka a smer chvostíka určujú rýchlosť a smer pohybu žubrienky. Počítačový model sa má riadiť troma základnými vlastnosťami:Každá žubrienka pritom vidí iba svojich najbližších susedov. Pridajte "dravca", teda inofarebnú žubrienku, ktorá sa pohybuje smerom k ostatným žubrienkam a ktorej sa žubrienky snažia vyhýbať.

Zobrazenie ”žubrienok” (čiernych bodov s ”chvostíkom”), ktoré sa pohybujú smerom vpravo nahor a vyhýbajú sa prekážke (kruhu).
(tému vypracuje A. Kružic)
Téma 14.
Standing Ovation. (Homework from Miching State University, see homepage http://zia.hss.cmu.edu/econ/homework95). Consider the following situation: Agents are seated in an auditorium listening to a brilliant economics lecture. At the end of the talk, after wiping away the tears, the applause begins, and perhaps a standing ovation ensues.Model, using whatever techniques you desire, the process of a standing ovation.
Suggest some in nature appearing scenarios that could be usefully modeled using such a process.
(tému vypracuje P. Kolenič, skúška 11. 2. 2000)
Téma 15
. Zobrazte sadu stavov jednorozmerného celulárneho automatu, kde sú bunky iba v jednom riadku (formálne spojenom do cyklu, t.j. začiatok riadku susedí s koncom) a možné stavy buniek 0 = biela, a 1 = čierna. Prechodové pravidlá pre stav buniek berú do úvahy iba momentálny stav bunky (v prostriedku) a jej ľavého a pravého suseda. Pravidlá sú zadané takto: 1,1,1 Ţ 1; 1,1,0 Ţ 1; 1,0,1 Ţ 1; 1,0,0 Ţ 0; 0,1,1 Ţ 1; 0,1,0 Ţ 0; 0,0,1 Ţ 0; 0,0,0 Ţ 1}. Napr. pravidlo 1,1,0 Ţ 1 znamená, že čierna bunka s čiernym ľavým a bielym pravým susedom bude v ďalšom časovom kroku čierna. Zobrazte sadu riadkov v časovej postupnosti, t.j. riadok v čase 0, pod ním riadok v čase 1 atď. Počiatočný stav riadku v čase 0 nech je generovaný náhodne. Zistite, po akej priemernej perióde sa riadky začínajú opakovať v závislosti na počtu buniek v jednom riadku. Vyskúšajte aj s inými sadami pravidiel.(tému vypracuje Peter Martinovic , skúška 4.2.2000 )
Téma 16
. Zostrojte model celulárneho automatu so 4 stavmi (na kvalite zobrazenia nezáleží, môže byť rozlíšené rôznofarebnými štvorčekami):Pravidlá: Na počiatku dvojrozmerná mriežka (na okrajoch spojená do toroidu, aby neboli problémy s ohraničením) obsahuje náhodne rozmiestené ihličie a mravce. Mravec sa pohybuje vždy náhodným smerom, no tak, aby dva mravce neboli v jednej bunke. Keď narazí na ihličie, zoberie ho. Keď mravec s ihličím narazí na iné ihličie, upustí svoje ihličie. (Môže tak aj z "kôpky" odoberať.)
Pozorujte, ako sa takýmto distribuovaným procesom budú vytvárať "kôpky", až nakoniec vznikne jedna veľká kopa. Zmerajte, ako dlho to priemerne trvá, kým je väčšina ihličia na jednej kôpke.
(tému vypracuje Peter Lalik, skúška dňa 21. 1. 2000)
Téma 17.
Použite viacčlenné evolučné stratégie pre nájdenie optima Rosenbrockovej funkcie. Program spustite 100´ a vypočítajte priemerný počet generácií, ktorý bol potrebný, aby najlepšia nájdená funkčná hodnota bola nižšia ako 10-6. Porovnajte to s priemerným počtom generácií, nutným k nájdeniu rovnakej funkčnej hodnoty, ale bez použitia kovariancie, teda bez použitia uhlu a . Podobne skúste odstrániť kríženie pri zachovaní použitia kovariancií a diskutujte vplyv tvaru alebo typu funkcie na efektívnosť použitia kríženia alebo kovariancie pri nájdení minima. (Symetria a multimodálnosť indikujú pravdepodobnú výhodnosť aplikácie kríženia, minimá uložené v ”údoliach” umiestnených naprieč k osiam súradnicového systému budú nájdené rýchlejšie pri použití kovariancií, čo platí aj pre ”viacrozmerné údolia”.)(tému vypracuje Eva Marinicová, skúška dňa 28.1. 2000)
Téma 18
. Zostrojte Hopfieldovu a Boltzmannovu sieť pre priradenie práce strojom vo fabrike (pozri kapitolu 11. pripravovanej knihy). Nech je M úkolov, N strojov, cena priradenia úkolu k pre stroj i je cik . Každý stroj i má celkové množstvo zdrojov bi, z ktorej sa úkolom k vyčerpá množstvo aik. Cieľom je minimalizovať cenu priradenia každého úkolu práve jednému stroju bez toho, že by sa prečerpal zdroj bi tohto stroja. Tento problém sa dá formálne popísať ako minimalizácia energie E![]()
s obmedzujúcimi podmienkami
![]() ,
,
![]()
kde xik = 0 alebo 1. Simulujte na počítači pre dáta v tabuľke, kde N=3, M=8, a aik = ak pre všetky i. (Každý uzol uik v sieti bude odpovedať priradeniu úkolu k pre stroj i, taký uzol môže byť alebo zapnutý alebo vypnutý). Ideálne optimum je vyznačené podčiarknutými hodnotami cik, suma týchto hodnôt je 57. V ideálnom prípade by teda mali byť aktivované uzly odpovedajúce podtrhnutým pozíciám.
|
Tabuľka: Vstupné hodnoty pre príklad 18 |
||||||||||
|
|
|
akI |
7 |
9 |
8 |
4 |
2 |
3 |
10 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
bi |
|
cik |
|
|
|
|
|
|
|
|
|
8 |
|
|
6 |
12 |
15 |
13 |
4 |
5 |
8 |
7 |
|
24 |
|
|
18 |
10 |
6 |
4 |
2 |
8 |
14 |
4 |
|
12 |
|
|
9 |
7 |
10 |
4 |
8 |
1 |
4 |
12 |
(tému vypracuje Svorad Štolc, skúšku absolvoval dňa 6.4.2000.)
Téma 19
. (This case study is taken from the home page of Prof. D. Goldberg). Simulate the convergence of a genetic algorithm with population sizes n = 25, 50, 100, 200 members under proportionate selection (i.e. a probability of selection is proportional to fitness) with simple replacement (no other operators like mutation and/or crossover are involved). The population should be initialized with one individual with fitness f = fmax and the remaining individuals with fitness f = 1. Take fmax = 1.5, 3, 9. Observe the time (in generations) required for the population to converge to n - 1 members of higher fitness. Repeat each run a minimum of 3 times with different random seeds. Repeat for tournament selection (with replacement). For the first set of runs use pairwise tournament selection (s =2) with pwinner = 1 (i.e. winner with a greater functional value is selected deterministically for the next generation) and run for all fitness cases. Thereafter run experiments with s = 1.5, 3, 9, using only fmax = 1.5.(tému vypracuje Peter Satury, skúšku absolvoval dňa 4.2.2000)
Téma 20
. Zobrazte evolúciu stratégií hry väzenská dilema, ktorá je modelovaná genetickým algoritmom, pričom každá dvojica väzňov bude interagovať vždy 10 krát medzi sebou. Tabuľka platieb je|
|
koooperuje (C) |
nekooperuje (D) |
|
kooperuje (C) |
3,3 |
0,5 |
|
nekooperuje (D) |
5,0 |
1,1 |
Napríklad keď prvý väzeň nekooperuje (D) a druhý väzeň kooperuje (C), prvý dostane 5 bodov a druhý 0 bodov. Väzni majú pamäť veľkosti 1, pamätajú si iba posledný ťah súpera. Napríklad stratégia CCD (chromozóm o troch zložkách) znamená: v prvom kroku agent kooperuje (1. položka v chromozóme je C), v ďalších ťa
hoch kooperuje (2. zložka je C), ak v predchádzajúcom ťahu súper kooperoval, alebo nekooperuje (3. zložka je D), ak súper v predchádzajúcom ťahu nekooperoval. Pri populácii 1000 urobte vždy náhodne 500 skupín po 10, nechajte ich všetky po dvojiciach interagovať medzi sebou, s tým, že sa každému budú sčitovať platby a zoberte do ďalšej generácie iba 2 najlepších. Výsledky má byť graf, kde na osi x bude číslo generácie (teda čas) a na osi y početnosť zástupcov tej ktorej stratégie v generácii.(tému vypracuje Radoslav Tausinger, skúška dňa 7.1.2000)
Téma 21
. Použitie genetického algoritmu na nájdenie maximálnej nezávislej množiny vrcholov.Nech G=(V,E) označuje graf kde V je množina vrcholov a E je množina neorientovaných hrán medzi dvojicami vrcholov. Problém je nájsť podmnožinu (maximálnej kardinality) množiny vrcholov, ktorej žiadne dva vrcholy nie sú spojené hranou. Vygenerujte náhodne vygenerované grafy s počtom vrcholov 100 a s predpísanou hustotou (sada 0,1 0,2 0,3 0,4 0,5), zobrazte pre najväčšiu nájdenú veľkosť priemernú, maximálnu a minimálnu hodnotu pre 100 behov programu. Zobrazte grafy pre rôzne parametre genetického algoritmu a pre rôzne typy ohodnocovania fitness pre závislosť počet ohodnotení fitness oproti najlepšej momentálnej hodnote. Diskutujte možnosť preklenúť Hammingov problém pre grafy typu dvoch lineárnych reťazcov typu,
6–7–8–9–10
1–2–3–4–5
kde sú spojené vrcholy ešte krížom, teda 6-2, 7-3, 8-4, 9-5 a 1-7, 2-8, 3-9, 4-10 a kde množiny
V´={1,3,5,6,8,10} a V´={2,4,7,9} sú globálnym a lokálnym minimom.Ako úvodnú literatúru použite
S. Khuri and Th. Baeck: An Evolutionary Heuristic for the Minimum Vertex Cover Problem (52k), J. Hopf,
editor: Genetic Algorithms within the Framework of Evolutionary Computation, pp. 86-90, Max Planck Institut
für Informatik, Saarbrücken, 1994.
at http://ls11-www.informatik.uni-dortmund.de/people/baeck/ea_application.html
(tému vypracuje Čestmír Hýbl ,skúška dňa 12.4.2000)
Vypracované "case studies" v šk.r. 1999/2000
1. Andrej Probst: Genetický algoritmus (ps.zip alebo pdf)
2. Pavol Droba: Tabu Search algoritmus Praca vo formate HTML
3. Peter Martinovič: Jednorozmerný celulárny automat (ps.zip alebo pdf, kompletná dokumentácia zip)
4. Radoslav Tausinger: Väzeňská dilema (ps.zip alebo pdf, program v Pascalu pas)
5. Ondrej Lonek: Adaptácia neurónovej siete pomocou genetického algoritmu (ps.zip alebo pdf, zdrojový kód zip, binárny kód zip, príklad zip )
6. M. Kubačák: Evolučná stratégia (1+1) (ps.zip alebo pdf, zdrojový kód pas.zip, príklad zip )
7. Peter Lalík: Model celulárneho automatu so 4 stavmi (ps.zip alebo pdf, zdrojový kód zip)
8. J. Kľuka: Simulované žíhanie pre riešenie úlohy obchodného cestujúceho na ortogonálnej mriežke (ps.zip alebo pdf, zdrojový kód zip)
9. Eva Mariničová: Použite viacčlenné evolučné stratégie pre nájdenie optima Rosenbrockovej funkcie (ps.zip alebo pdf, zdrojový kód zip)
10. Peter Kolenič: Modelovanie "Standing ovations" (ps.zip alebo pdf.zip, zdrojový kód zip, exe súbor zip)
11. Peter Satury: Simulačné výpočty konvergencie GA (ps.zip)
12. Ján Borovský: Genetické programovanie, symbolická regresia a boolovské funkcie (ps.zip alebo pdf)
13. Svorad Štolc: Hopfieldove neurónové siete a ich základné vlastnosti (ps.zip alebo pdf)
14. Čestmir Hýbl: Aproximácia maximálnej nezávislej množiny vrcholov grafu pomocou GA (ps.zip alebo pdf)