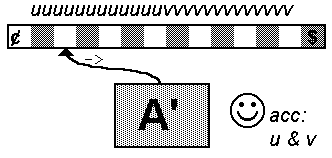
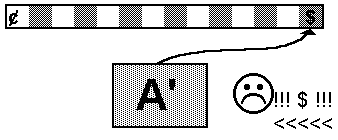
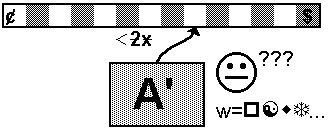
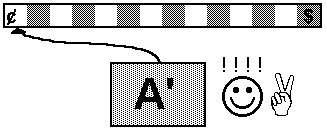
Keďže jazyk L je regulárny, existuje deterministický konečný automat, ktorý ho akceptuje. Nech teda automat A akceptuje náš regulárny jazyk L.
A = (K,S,d,q0,F), kde množina stavov K = (q0,q1,…,qk), vstupná abeceda je S, d je prechodová funkcia, q0 je počiatočný stav a F je množina akceptačných stavov.
Našou snahou je teda dokázať, že jazyk L' je tiež regulárny. A taktiež vieme, že nedeterministické konečné dvojsmerné automaty sú schopné rozpoznávať triedu regulárnych jazykov ( podobne, ako automaty DKA a NKA) (V skutočnosti príslušná veta znie takto: " Trieda jazykov akceptovaná dvojsmerným deterministickým konečným automatom je R". My síce teraz pracujeme s nedeterministickým kon. automatom, ale predošlé tvrdenie sa dá zovšeobecniť pre všetky dvojsmerné kon. automaty.). Skonštruujme teraz nedeterministický dvojsmerný automat tak, aby prvé dve tretiny vstupného slova rozpoznával na základe automatu A, a chýbajúcu zvyšnú tretinu by nedeterministicky uhádol.
A' = (K',S,D ,q0,F'), kde
K' = K Č {qa' (" qa Î K)} Č {qaL' (" qa Î K)} Č {qFINAL} (qa' a qaL' sú tzv. cúvajúce stavy)
S' = S (lebo pracujeme nad tou istou abecedou)
q0 =q0
F' = {qFINAL}
D(qa,x) = {(qb,1)} Ű d(qa,x) = qb & xÎ S'
D(qa,$) = {(qa',-1)}
D(qa',x) = {(qaL',-1)} xÎ S'
D(qaL',x) = {(qb',-1)} Ű d(qa,y) = qb "yÎ S' & xÎ S'
D(qa',¢) = {(qFINAL,1)} ak qaÎF
D(qFINAL,x) = {(qFINAL,1)} "xÎ S'
Automat pracuje nasledovne:




