Charakteristika dobre sifry

Mnozstvi prace vynalozene na sifrovani a desifrovani by melo byt umerne pozadovanemu stupnu utajeni.
Sifrovaci algoritmus by nemel obsahovat zbytecna omezeni.
Implementace algoritmu by mela byt co nejjednodussi.
Chyby pri sifrovani by se nemely prilis sirit a ovlivnovat nasledujici komunikaci.
Zpravy by se zasifrovanim nemely zvetsovat.

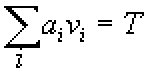
Zmateni (confusion) - nelze predikovat, jakou zmenu zasifrovaneho textu vyvola byt jen mala zmena otevreneho textu <=> slozita funkcni zavislost mezi zasifrovanym textem a parem klic - otevreny text.
Difuze(diffusion) - zmena otevreneho textu se promita do mnoha mist zasifrovaneho textu.
Bezpecny system - nelze ziskat otevreny text na zaklade znalosti odpovidajici sifry

kryptoanalytik hleda transformaci h : C->P, h nebyva jednoznacna

Efektivne bezpecny system - Prob(h(C) = P) < e.

Idealni stav

Perfektni utajeni (perfect secrecy) - mejme n moznych otevrenych textu, stejne mnozstvi klicu a moznych sifer.

Prob_C₁(h(C₁) = P) = Prob(h(C₁) = P) = Prob(P)

Redundance

pocet bitu nutny k reprezentaci vsech znaku abecedy A je horni cela cast z log₂(k)
pocet vsech moznych zprav delky n = 2^An, z toho 2^Rnsmysluplnych. R nazyvame rate jazyka. Redundance je definovana
D = A - R

Pokud algoritmus sifruje nekolik ruznych zprav, z nichz jedna je smysluplna, do stejne sifry, system muze byt bezpecny.

Public-key systemy (systemy s verejnym klicem)

pouzitii jednosmernych (trapdoor) funkci - snadno vycislitelna funkce, jejiz inversni funkci lze efektivne spocitat pouze se znalosti (maleho) mnozstvi dodatecnych informaci. Nezavisle na zprave.

kazdy uzivatel vlastni par klicu:

verejny (public) klic - znam vsem uzivatelum systemu, pouziva se k sifrovani zprav zasilanych tomuto uzivateli

tajny, soukromy (private) klic - uzivatel uchovava v tajnosti, pouziva jej k desifrovani doslych zprav
tajny klic nelze efektivne odvodit ze znalosti odpovidajiciho verejneho klice

vyhodou systemu s verejnymi klici je relativne male mnozstvi pouzivanych klicu, moznost vytvareni verejne overitelnych elektronickych podpisu, vetsi flexibilita spravy klicoveho materialu

Merkle-Hellman system

zalozen na problemu batohu, prenasena zprava je chapana jako vektor reseni, prenasena je vysledna suma - "hmotnost batohu"

a₁, a₂, ... a_n - posloupnost celych cisel, T cilova suma = hmotnost batohu, hledame vektor v takovy, aby

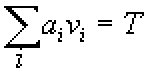
necht posloupnost a₁, a₂, ... a_n je superrostouci, problem nalezeni vektoru v je v tomto pripade zvladnutelny v linearnim case

Konstrukce systemu

zvolime superrostouci posloupnost s₁, s₂, ... s_n, dale vybereme cislo w a modul m,
w bereme nesoudelne s m, m > s_n.

Ze zvolenych hodnot sestavime jiz obecnou posloupnost

h_i = w_*s_i mod m

Posloupnost {s_i}_i=1..n a cisla w a m utajime, dale budou slouzit jako soukromy klic.
Posloupnost {h_i}_i=1..n zverejnime jakozto verejny klic.

Sifrovani

Otevreny text P rozdelime na bloky delky n bitu.
Kazdy blok P_j nahradime sumou
Zasifrovany text C odesleme

Desifrovani

Autorizovany prijemce vypocita w^-1 - z vlastnosti w a m urcite existuje.
Pro kazdy blok C_j spocita C_j _* w^-1.
Vyresi problem batohu se superrostouci posloupnosti {s_i}_i=1..n pro vsechny hodnoty ziskane v predchozim bode.
Konkatenaci reseni vznikne puvodni zprava P.

Korektnost desifrovani

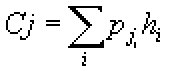
w^-1e(p) mod m

= w^-1(p₁h₁+p₂h₁+ ... +p_nh_n) mod m =
= p₁w^-1h₁+p₂w^-1h₁+ ... +p_nw^-1h_n mod m =
= p₁w^-1ws₁+p₂w^-1ws₁+ ... +p_nw^-1ws_n mod m =
= p₁s₁+p₂s₁+ ... +p_ns_n mod m.

Poznamky k implementaci

Pro rozumne aplikace:

m byva voleno ve velikosti 100 az 200 cislic,
s_i maji delku 200 az 400 cislic,
batoh miva priblizne 200 polozek

Mozny zpusob vytvoreni superrostouciho batohu:

vygenerujeme n nahodnych cisel r_i z intervalu <0, 2²⁰⁰>
s_i = 2^{200 + i - 1} + r_i

Analyza Merkle-Hellmanova systemu

Zname-li m, je mozne odvodit prvky superrostouciho batohu.

Polozme

p = h₀ / h₁ mod m

Pak ovsem plati

p = (w_*s₀ )/(w_*s₁ ) mod m = s₀ / s₁ mod m

Spocitame posloupnost

D = {i _* p mod m}_i=1..2ⁿ

Pro nejake k ovsem nastane

k_*p mod m = k_*s₀_*1/s₁ mod m = s₀

Lze ocekavat, ze s₀ bude nejmensim prvkem d. Zname-li s₀, lze spocitat w a tedy vsechny s_i.
Hodnoty w a m je mozne odhadovat pouze z posloupnosti {h_i}_i=1..n. Hodnota m je vetsi nez libovolne h_i. Budeme zkouset ruzne hodnoty pro w.

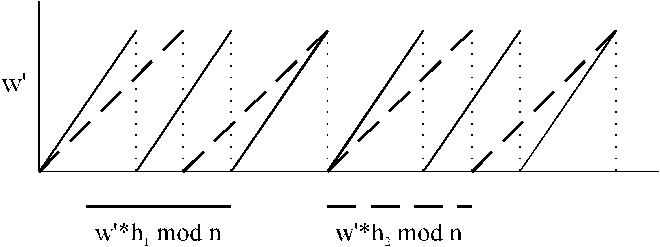
Graf (w'<SUB>*</SUB>H1 mod n) a (w'<SUB>*</SUB>H2 mod n)

Mozne spravne hodnoty w se nachazeji v prekryvajicich se bodech diskontinuity.

K prolomeni Merkle-Hellmanova systemu tedy neni nutne vyresit obecny problem batohu, ale staci pouzit naznaceneho postupu, ktery je daleko rychlejsi. M-H system tedy neni vhodny k ochrane dulezitych informaci.

Rivest-Shamir-Adelman kryptosystem

uverejneny v roce 1977. Uvedeme modifikaci oznacovanou jako kod Herkules, jez je v soucasne dobe pouzivana Ministerstvem obrany USA pro prenos utajovanych informaci vysoke dulezitosti.

Kryptoschema je zalozeno na Eulerove formuli

a ^f(n) = 1 mod n (1)

kde f(n) je pocet cisel z intervalu 1,..,n, ktera jsou s n nesoudelna.

Plati:

f(n) = (p₁ - 1)p₁^a₁-1_* (p₂ - 1)p₂^a₂-1_*..._* (p_k - 1)p_k^a_k-1 (2) kde n = p₁^a₁_* p₂^a₂_*..._* p_k^a_k (3) je prvociselny rozklad cisla n.

Sifrovani

je treba znat cislo n a male prvocislo e.
Otevreny text P prevedeme na posloupnost cisel modulo n.
Kazdy blok P_j zasifrujeme dle vzorce C _j = P_j^e mod n (4) Spojenim vyslednych bloku C_j vznikne zasifrovany text.

Desifrovani

je treba znat cislo n, a cislo d.
Kazdy z bloku C_j desifrujeme takto:

P _j = C_j^d mod n (5)

Vypocet desifrovaciho klice d

Musi platit ed = 1 mod f(n) (6)

Prvocislo e nesmi delit (f(n)). Nalezneme

r = -f(n)^e-2 mod e (7)

Ze (2) plyne f(e) = e-1, s pouzitim (1)

rf(n) = -f(n)^f(e) = -1 mod e (8)

Polozime tedy

d = (rf(n)+1) / e (9)

Korektnost desifrovani

S pouzitim (1) a (6) postupne dostavame

P_j^ed = P_j^{ed mod f(n)} = P_j¹ = P_j (mod n)

Vyber klicu, implementacni poznamky

Verejny klic tvori par (n, e), soukromy klic par (n, d).
cislo n musi byt velmi velke, nesmi mit male faktory. Pro realne pouziti priblizne 100 az 200 cislic.
Necht n je soucinem prvocisel p a q. Klic e volime jako prvocislo vetsi nez (p - 1) a (q - 1).
Pri teto volbe ma nepritel na vyber zhruba (n^1/2/ln n) - (10⁵⁰/100 ln 10) moznych prvociselnych cinitelu.

Volba prvocisel

Vygenerujeme nahodne liche cislo zvoleneho radu
Otestujeme prvociselnost
Neni-li prvocislo, pokracujeme bodem 1.

Solovay-Strassenuv test prvociselnosti

Pokud p je cislo, ktere zkoumame a r libovolne cislo, pak nutne

nsd(p, r) = 1

a zaroven

J(r, p) = r ^p-1/2 mod p

kde J(r, p) je Jacobiho funkce, definovana nasledovne

/ 1 pro r = 1

J(r, p) = - J(r/2, p)_*(-1)^(p²-1)/8 pro r sude

\ J(p mod r, r)_*(-1)^(r-1)(p-1)/4 pro r liche

Milleruv test prvociselnosti

Dano testovane cislo p.

Necht p - 1 = 2^ls, pro nejake liche s
Nahodne zvolime a z {1, 2, ... , p - 1}
Spocitame q = a^s mod p. Pokud q = 1 mod p => konec, p je asi prvocislo.
Pocitame q¹, q², ..., q^{2^l}, = a^p-1 mod p. Pokud neni a^p-1 = 1 mod p => konec, p nemuze byt prvocislo.
Nalezeme nejvetsi k tak, ze q^{2^k} neni 1 (mod n). Pokud q^{2^k} = -1 mod p => konec, p je asi prvocislo
p nemuze byt prvocislo.

Analyza RSA

Dodnes neni znama metodas vedouci k rozbiti tohoto algoritmu. Jedinou slabosti je hypoteticka moznost vytvorit elektronicky podpis zpravy bez znalosti desifrovaciho klice na zaklade zachyceni vhodnych predchozich zasifrovanych zprav.
M^dL^d = (ML)^d

System LUC

zalozen na Lucasovych funkcich, ktere lze chapat jako zobecneni mocnin

Lucasovy funkce

jsou prikladem linearnich rekurenci vyssiho radu. Necht P₁, P₂, P₃, ... , P_m jsou cela cisla. Definujeme {T_n}: T_n = P₁T_n-1 + P₂T_n-2 + K + P_mT_n-m T₀, T₁, T₂, ... T_m, dodefinujeme nezavisle.

Obecna linearni rekurence druheho radu:

T_n = PT_n-1 - QT_n-2 (1)

P a Q nesoudelna cela cisla. Necht x₁ a x₂ jsou koreny rovnice

x² + Px + Q = 0 (2)

Jsou-li c₁ a c₂ lib. cisla, plati pro posloupnost {c₁x₁ⁿ + c₂x₂ⁿ}

P(c₁a^n-1) + c₂b^n-1 - Q(c₂a^n-2 + c₂b^n-2) = c₁a^n-2(Pa - Q) + c₂b^n-2(Pb - Q) =
= c₁a^n-2a² + c₂b^n-2b² =
= c₁aⁿ + c₂bⁿ

Zajimave linearni rekurence:
Uⁿ = (aⁿ - bⁿ) / (a - b), (tedy c₁ = -c₂ = 1/(a - b) )
Vⁿ = aⁿ + bⁿ, (tedy c₁ = c₂ = 1 )

Polozime-li U₀ = 0, U₁ = 1, V₀ = 2, V₁ = P jde o posloupnosti celych cisel, ktere nazyvame Lucasovymi funkcemi P a Q.

Vlastnosti Lucasovych funkci

D diskriminant (2), a a b koreny (2). Potom
a + b = P, ab = Q, a D = (a + b)²

Dale plati
V_2n = V_n² - 2Qⁿ        (3)
V_2n-1 = V_n²V_n-1² - PQ^n-1        (4)
V_2n+1 = PV_n² - QV_n²V_n-1² - PQⁿ        (5)
V_n² = DU_n² + 4Qⁿ        (6)
2V_n+m = V_nV_m + DU_nU_m        (7)
2Q^mV_n-m = V_nV_m - DU_nU_m        (8)
P nahradime V_k(P,Q) a Q nahradime Q^k:
T_n=V_k(P,Q)T_n-1 - Q^kT_n-2.

Koreny odpovidajici rovnice, a' a b', splnuji
a' + b' = V_k(P,Q) = a^k + b^k a a'b' = Q^k = a^kb^k,
tedy a' = a^k a b' = b^k (a vice versa). Muzeme ziskat

V_n(V_k(P, Q), Q^k) = (a^k)ⁿ + (b^k)ⁿ = a ^nk + b ^nk = V_nk(P, Q)

Polozme Q = 1:

V_n(V_k(P, 1), 1) = (a^k)ⁿ + (b^k)ⁿ = a ^nk + b ^nk = V_nk(P, 1) (9)

Dale budeme definovat Legendruv symbol:

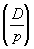= 0 prave kdyz p deli D, jinak
= 1 pokud existuje cislo x tak, ze D = x² mod p
= -1 pokud zadne takove x neexistuje.

Necht p prvocislo nedelici Q a D, a e je rovno [Legendruv symbol (D / p)]

. Pak lze dokazat:
U_k(p-e)(P, Q) = 0 mod p (10)
V_k(p-e)(P, Q) = Q^k(1-e)/2 mod p (11)
pro libovolne cele k.
Dale zavedeme Lehmerovu funkci pro cisla tvaru N = pq, p a q jsou prvocisla:
T(N) = (p-)(q-)
Neni nutny cely soucin.
S(N) = NSN((p-), (q-))
.

S(N) je nasobkem (p-)   i   (q-), N = pq, p a q jsou ruzna prvocisla nedelici D = P² - 4, s pouzitim (10) a (11):
U_kS(N)(P, 1) = 0 mod p        (12)
V_kS(N)(P, 1) = 2 mod p        (13)
pro libovolne cele k.
Pokud navic e je libovolne cislo nesoudelne s S(N), d zvolime tak aby
ed = kS(N) + 1 pro vhodne k, potom:

V_d(V_e(P, 1), 1) = V_de(P, 1)   podle (9)

= V_kS(N)-1(P, 1)

= PV_kS(N)(P, 1) - V_kS(N)-1(P, 1)   podle (1)

= PV_kS(N)(P, 1) - 1/2(V_kS(N)(P, 1)V₁(P, 1) - DU_kS(N)(P, 1)U₁(P, 1))   podle (8)

= 2P - 1/2(2P - 0)) mod N   podle (12), (13)

= P (14)

LUC kryptosystem

Zvolime N , e. N soucinem prvocisel p a q.
e musi byt nesoudelne s (p - 1) (q - 1) (p + 1) (q + 1).
M - zprava, mensi nez N, nesoudelna s N.

Sifrovani

f_LUC(M) = V_e(M, 1) mod N
Vysledkem je zasifrovana zprava M'.

Desifrovani

K desifrovani potrebujeme d splnujici:
de = 1 mod S(N)
kde
S(N) = NSN((p-), (q-))
. .
Zde [Legendruv symbol (D / p)]

jsou Legendrovy symboly pro D vzhledem k p a q .
Predpokladame D je nesoudelne s N , tedy Legendrovy symboly jsou 1 nebo -1, e je nesoudelne s S(N) a tedy d existuje.

Desifrovani odpovida sifrovani kde e nahradime d.

Korektnost desifrovani

Podle (14) lze overit:
M = V_d(V_e(M, 1) mod N, 1) mod N

	/	1	pro r = 1
J(r, p) =	-	J(r/2, p)_*(-1)^(p²-1)/8	pro r sude
	\	J(p mod r, r)_*(-1)^(r-1)(p-1)/4	pro r liche

V_d(V_e(P, 1), 1)	= V_de(P, 1)	podle (9)
	= V_kS(N)-1(P, 1)
	= PV_kS(N)(P, 1) - V_kS(N)-1(P, 1)	podle (1)
	= PV_kS(N)(P, 1) - 1/2(V_kS(N)(P, 1)V₁(P, 1) - DU_kS(N)(P, 1)U₁(P, 1))	podle (8)
	= 2P - 1/2(2P - 0)) mod N	podle (12), (13)
	= P		(14)