Secret key systemy (systemy s tajnym klicem)
stejny klic je pouzit pro sifrovani i desifrovani
Mnoho z dnes pouzivanych systemu jsou Feistelovy sifry.
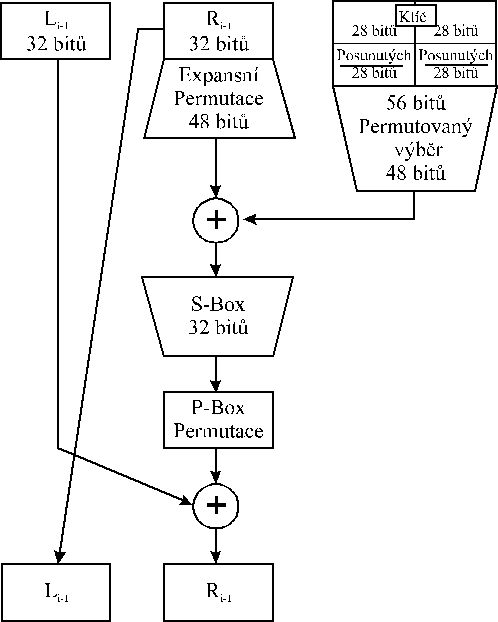
Obecny tvar jednoho cyklu Feistelovy sifry:
Kryptosystem DES
Vyvinula firma IBM na zakazku NBS pocatkem
70. let. Puvodni nazev DEA, v USA DEA 1. Jako
standard prijat 23. 11. 1976
Dodnes pouzivan v komercni sfere,
pro vojenske ucely neni certifikovan
ani pro ochranu neklasifikovanych informaci. Patrne
nejrozsahleji pouzivany sifrovaci
algoritmus vsech dob.
Norma ANSI X3.92
Sifruje 64 bitove bloky otevreneho textu na
na stejne dlouhe bloky vystupni, delka
klic 64 bitu, z toho nezavislych bitu je
56.
Pozadavky zadavatele
- Algoritmus musi poskytovat vysoky stupen ochrany
- Musi byt formalne popsatelny
a snadno pochopitelny
- Bezpecnost algoritmu nesmi zaviset na
znalosti ci neznalosti samotneho algoritmu.
- Musi byt dostupny pro nejsirsi
verejnost.
- Musi byt pouzitelny v nejruznejsich
aplikacich.
- Musi byt efektivni.
- Musi byt overitelny.
- Musi byt exportovatelny.
Rezimy cinnosti
- ECB (electronic code book) - pouze sifrovani klicu
C = E(K, P)
- CBC (cipher block chaining) - vhodny pro sifrovani zprav
Cn = E(K, Pn xor Cn-1)
- CFB (cipher feed back) - pro sifrovani podobne proudovym sifram
Cn = Pn xor E(K, shl(Reg, k) + left(Cn-1, k))
- OFB (output feed back) - pro aplikace, kdy je treba eliminovat sireni prenosovych chyb, vysokokapacitni spoje s velkou redundanci (rec, video)
Hn = E(K, shl(Reg, k) + left(Hn-1, k))
Cn = Pn xor Hn
Analyza
- uvodni permutace nema prakticky zadny vliv
- prilis kratky klic (efektivne pouze 56ti bitovy)
- komplementarnost
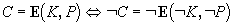
- existence slabych (weak) klicu E(K) = D(K)
a poloslabych klicu E(K1)E(K2) = Id
- nevhodny navrh S-boxu
Mozne zpusoby zvyseni bezpecnosti
- vicenasobne sifrovani - nestaci dvojnasobne ke skutecnemu zvyseni bezpocnosti nutno sifrovat
C = E(K1)D(K2)E(K1)
- zvyseni delky hesla na 768 bitu (neprilis ucinne)
Sifrovani
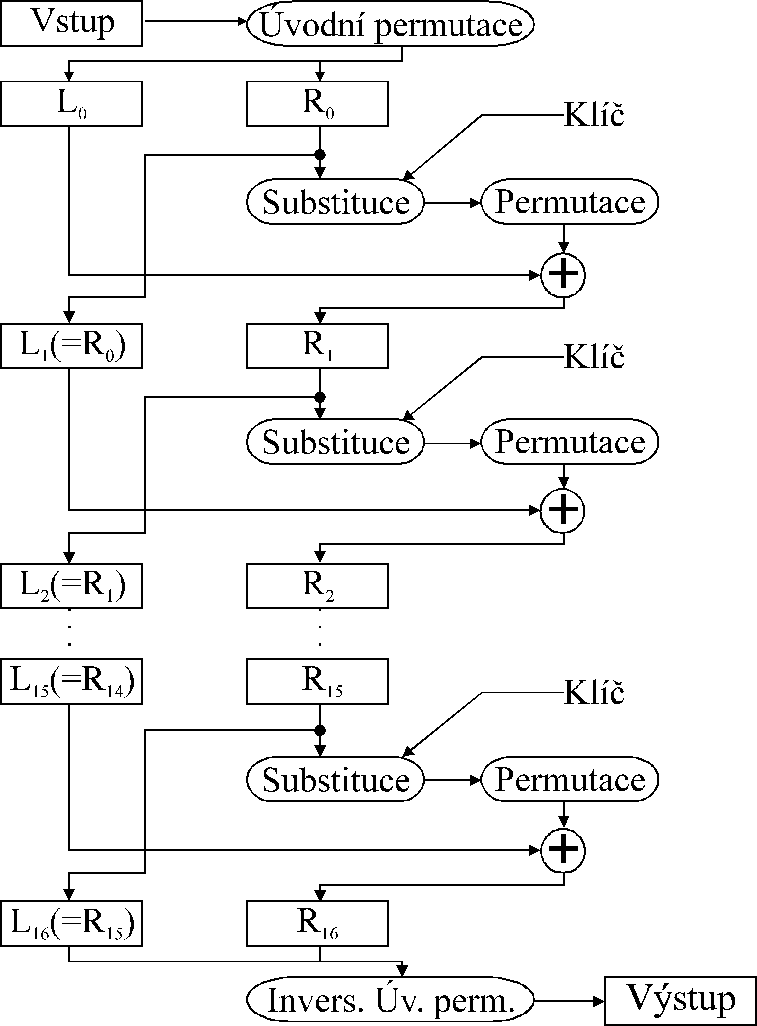
Uvodni permutace:
Vlastni sifrovani:
System Blowfish
Opet Feistelova sifra, delka bloku 64 bitu, promenna delka klice az 448 bitu
Subklice
predpocitavaji se pred kazdym sifrovanim
- P-pole = 32 bitove klice
- pole S-boxu. kazdy 256 32bitovych polozek
S1,0, S1,1, ... S1,255
S2,0, S2,1, ... S2,255
S3,0, S3,1, ... S3,255
S4,0, S4,1, ... S4,255
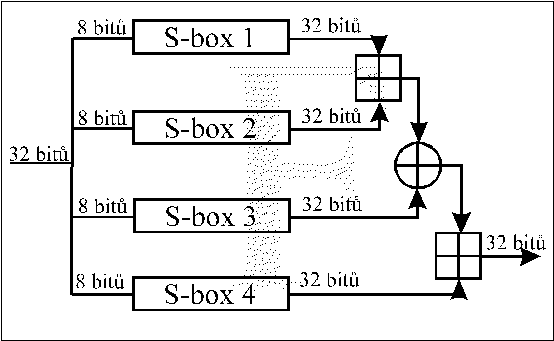
Nereverzibilni funkce F
F(xL) = ((S1,a + S2,b mod 232) xor S3,c) + S4,d mod 232
xL = a|b|c|d
Generovani podklicu
- Inicializujeme P-pole a vsechny S-boxy pevnym retezcem
- xor P1 s prvnimi 32 bity klice, xor P2 s dalsimi 32 bity klice atd.
- Zasifrujeme nulovy retezec
- P1 a P2 nahradime vystupem predchoziho kroku
- Zasifrujeme vystup kroku 3
- P3 a P4 nahradime vystupem predchoziho kroku
- Stejne pro ostatni polozky P-pole a vsechny S-boxy
Algoritmus provadi 16 cyklu nad vstupem delky 64 bitu.
Pro ucely analyzy byly navrzeny jeho zmensene varianty (MiniBlowfish)
pracujici nad vstupem 32 resp. 16 bitu.
Sifrovani systemem Blowfish:
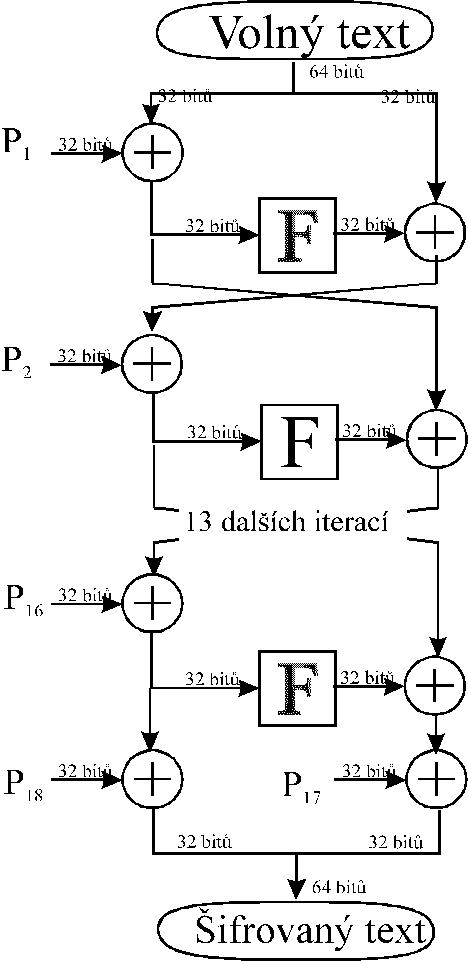
Jedna F transformace:
Kryptosystem VINO
blokova sifra, blok 64bitu, klic 128 bitu
Veta(Vinogradov):
Necht m, n jsou cela cisla. Uvazujme poslouonist 1, 2, ..., n,
n, n-1, ..., 2, 1, 2, ..., n, n-1, ... Z teto posloupnosti postupne
vybirame 1., (m+1), (2m+1), ... prvek az ziskame
n cisel. Popsanou operaci opakujeme se ziskanymi cisly.
Vysledkem k-teho opakovani bude puvodni
retezec cisel prave kdyz

- vybiranim uvedenym postupem s krokem m z posloupnosti Pn ziskame posloupnost P'n.
- inverzni postup spociva ve vybirani z posloupnosti P'n s krokem mk-1
Popsany postup muze byt pouzit k permutaci retezce, celkovy pocet takto ziskanych permutaci je n.
Zlepseni:
oznacme P - sekvenci, kterou chceme permutovat a K klic
K rozdelime na ctyri casti a provedeme nasledujici postup:
- vybime z P s krokem m, kde m je rovno prvni casti K. Ziskame P'
- provedeme cyklicky posuv P' rizeny druhou casti K. Ziskame P''
- krok 1. opakujeme pro P'' a treti ca K, ziskame P'''
- krok 2. opakujeme pro P''' a ctvrtou ca K, ziskame P'''
Popsany postup oznacujeme V-permutace
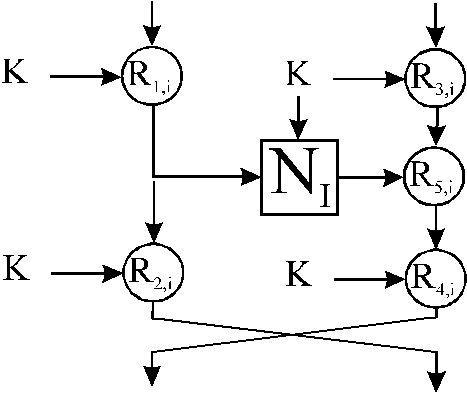
Schema cyklu
oznacme  bitove xor
a
bitove xor
a  scitani celych cisel modulo 2n.
Vstup cyklu podrobime V-permutaci, vysledek rozdelime na ctyri bloky po 16ti bitech.
scitani celych cisel modulo 2n.
Vstup cyklu podrobime V-permutaci, vysledek rozdelime na ctyri bloky po 16ti bitech.
Vypocet probiha v souladu s nasledujicim obrazkem:
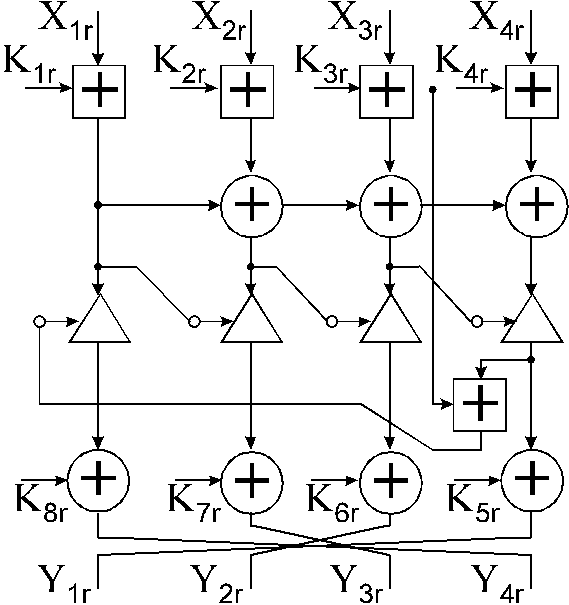
Tvorba podklicu
V prvnim cyklu je podklic cyklu K1 roven klici K.
Dalsi klice jsou ziskany nasledujicim zpusobem:
- provedeme V-permutaci klice Kj-1 rizenou klicem Kj-1, ziskame K'j-1
- ucinime posuv Kj-1 o jeden bit vlevo, zprava doplnime 0 a invertujeme sude bity , ziskame K''j-1
- Kj = K'j-1
 K''j-1.
K''j-1.
Celkove schema
Algoritmus nejprve nad vstupni zpravou provede t cyklu
a na zaver jeste jednu V-permutaci rizenou klicem Kt.
Pro rozumnou miru bezpecnosti staci t = 4.
Analyza
Algoritmus byl publikovan v roce 1993, dosud neni znama analyza.
Proudove sifry
zpracovavaji otevreny text po jednotlivych bitech
System Fish
proudova sifra zalozena na Fibonacciho generatoru pseudonahodnych cisel
Vypoustejici generatory (shrinking generators)
predp. dva generatory pseudonahodnych cisel A a S.
A generuje posloupnost a0, a1, ... prvku GF(2)nA
S obdobne posloupnost s0, s1, ... prvku GF(2)nS
dale budeme pouzivat funkci d: GF(2)nS -> GF(2)
Vypoustejici procedura ponecha k dalsimu zpracovani prvky ai a si pokud
d(si)=1
aplikaci vypousteci procedury ziskame posloupnosti
z0, z1, ...
z a0, a1, ...
h0, h1, ... resp. z s0, s1, ...
Popis algoritmu Fish
zvolime nA, nS rovno 32
jako A i S budeme pouzivat uzavreny Fibonacciho generator
ai = ai-55 + ai-24 mod 232
si = si-52 + si-19 mod 232
Samozrejme prvky a-55, a-54, ..., a-1 musi
byt vhodnym zpusobem odvozeny z klice. Obdobne pro posloupnost si.
Funkce d mapuje 32-bitovy vektor na jeho nejmene vyznacny bit.
Neni bezpecne pouzivat k sifrovani poimo
posloupnost z0, z1, ... :
s pravdepodobnosti 1/8 totiz trojice
ai, ai-55, ai-24
projde cela do posloupnosti {zi}
rozdelime posloupnost z0, z1, ...
na pary (z2i, z2i+1),
h0, h1, ... na pary
(h2i, h2i+1) a vypocitame
vysledne hodnoty r2i, r2i+1:
c2i = z2i  (h2i
(h2i  h2i+1)
h2i+1)
d2i = h2i+1 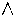 (c2i
(c2i  z2i+1)
z2i+1)
r2i = c2i  d2i
d2i
r2i+1 = z2i+1  d2i
d2i
Jako tradicne  znaci xor,
znaci xor,
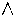 oznacuje bitove and.
oznacuje bitove and.
Protoze h2i, h2i+1 maji nejnizsi
bit jednickovy, je vhodne nastavovat nejnizsi bit z2i, z2i+1
v zavislosti na hodnote r2i, r2i+1.
Sifrovani se provadi napr. xorovanim vysledne posloupnosti s otevrenym textem.
Analyza
Algoritmus byl publikovan koncem roku 1993, dodnes neni znama analyza.
© Tonda Benes, 1995
S prevodem tohoto dokumentu do HTML pomahal ©Dan Lukes, 1995
Toto je revision 1.0, 29.11.95
Tuto stranku shledlo jiz
 zvedavcu ...
zvedavcu ...


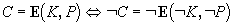





 bitove xor
a
bitove xor
a  scitani celych cisel modulo 2n.
Vstup cyklu podrobime V-permutaci, vysledek rozdelime na ctyri bloky po 16ti bitech.
scitani celych cisel modulo 2n.
Vstup cyklu podrobime V-permutaci, vysledek rozdelime na ctyri bloky po 16ti bitech.
 K''j-1.
K''j-1.
 (h2i
(h2i 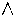 h2i+1)
h2i+1)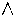 (c2i
(c2i  z2i+1)
z2i+1) d2i
d2i d2i
d2i znaci xor,
znaci xor,
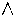 oznacuje bitove and.
oznacuje bitove and.