Kryptograficke hasovaci funkce - MAC, MDC kody

casto staci pouze autentizace puvodu ci obsahu zpravy, pripadne overeni integrity
ne vzdy staci k zajisteni techto pozadavku vlastni sifrovaci algoritmus

Pouziti

symetricke systemy - slouzi k rozpoznani pravosti desifrovane zpravy
asymetricke systemy - rychlejsi autentizace: spocita se hasovaci funkce nad danou zpravou a elektronicky se podepise az vysledny hashkod
ochrana hesel a passphrases

Zavisi-li vypocet hasovaci funkce na tajnem klici, oznacujeme tuto funkci jako MAC (message authentization code). Pokud takovy klic pouzit neni, jde o MDC (manipulation detection code).

Formalni definice

MAC je funkce h splnujici

zatimco argument X muze byt libovolne delky, vysledek h(K, X) ma pevnou velikost n ( n = 32 .. 64)
pro dane h a X je tezke urcit h(K, X) s pravdepodobnosti uspechu vyrazneji prevysujici 1/2ⁿ.
i se znalosti velkeho mnozstvi zvolenych paru {Xi, h(K, X_i)} musi byt tezke urcit K, nebo spocitat h(K, X) pro X X_i .

MDC casto delime na dve skupiny - OWHF, CRHF

Funkci h oznacime za OWHF (one-way hash function) prave kdyz:

zatimco argument X muze byt libovolne delky, vysledek h(X) ma pevnou velikost n ( n > 63)
pro dane Y a h musi byt tezke nalezt X aby Y = h(X)
pro dane X a h(X) musi byt tezke najit X' aby h(X) = h(X')

CRHF (collision resistant hash function) je takova funkce, ktera splnuje:

h je OWHF ( n > 127)
musi byt tezke najit par X', X'', tak, aby h(X') = h(X'')

Navrhy MDC funkci

prakticky vsechny zname hasovaci funkce pracuji nad vstupem pevne delky
iterovane hasovaci funkce (iterated hash f.) - delsi vstup X je zpracovavan opakovanim vypoctu H₀ = IV H_i = f(X_i, H_i-1) i = 1, 2, ..., t h(X) = H_t IV - inicializacni hodnota

casto delka vstupu neni nasobkem delky vstupniho bloku -> nutne zarovnani (padding)
zarovnani by melo byt jednoznacne (unambiguous) - nesmi dve ruzne zpravy doplnit na stejnou, je vhodne, aby na konec zpravy zapisovalo delku

Tvrzeni
Pokud zarovnani obsahuje delku vstupni zpravy a tato je dlouha alespon 2 bloky, potom nalezeni kolidujiciho vzoru h pri pevnem IV vyzaduje 2ⁿ operaci prave kdyz nalezeni kolidujiciho vzoru f pri libovolnem H_i-1 vyzaduje 2ⁿ operaci.

Tvrzeni
Predpokladejme jednoznacne zarovnani obsahujici delku vstupni zpravy. Je-li f odolna vuci kolizim (collision resistant), je h CRHF.

Hasovaci funkce zalozene na blokovych sifrach

vyhodne z hlediska navrhu a implementace
vetsina schemat ekvivalentni s jednim z nasledujicich

Matyas, Meyer, Oseas

f = E(s(H_i-1), X_i) delka hashkodu odpovida delce vstupu, E(K, X) = E(K, X) X.
ISO/IEC 10118 p. 2

Preneel, Govaerts, Vandenwalle

f = E(s(H_i-1), X_i) H_i-1 v obou pripadech E je libovolna blokova sifra, s je funkce mapujici prostor zasifrovanach bloku do prostoru klicu. Tyto funkce mohou byt CRHF pokud delka bloku je alespon 128 bitu. Bezpecnost umerna hodnote min(k,r).

MDC-2

funkce dava hashkod dvojnasobne delky vstupu, vhodna pro implementaci CRHF pomoci DES.
Obcas pod nazvem Meyer-Schilling T1_i = E(H1_i-1, X_i) = LT1_i || RT1_i T2_i = E(H2_i-1, X_i) = LT2_i || RT2_i H1_i = LT1_i || RT2_i H2_i = LT2_i || RT1_i H1₀ a H2₀ iniciovany hodnotami IV₁ resp. IV₂ , vysledek vznikne konkatenaci H1_t a H2_t .

MDC-4

jeden krok se sklada ze dvou iteraci MDC-2, jako vstup druhe iterace se pouzije H2_i-1 a H1_i-1.

Dosud neni znama mira bezpecnosti obou predchozich funkci, ani utok proti nim. Vydrzi patrne 5 - 10 let.

Hasovaci funkce zalozene na modularni aritmetice

nejlepsi schemata zalozena na umocnovani na druhou modulo n f = (X_i H_i-1)² mod N X_i pouzitim vetsiho mnozstvi operaci lze jeste zvysit bezpecnost f = (H_i-1 xor

(X_i)²)² mod N

Hasovaci funkce zalozene na problemu batohu

zatim neni jasne, zda problem batohu je tezky pouze v nejhorsim pripade, nebo zda je tezky v prumernem pripade
prakticky vsechny systemy zalozene na problemu batohu byly prolomeny

Specialni MDC funkce

algoritmy navrhovane od pocatku jako vypocet hasovacich funkci a potazmo MDC

obvykle vykonnejsi

MD4, MD5

MD4 navrzen Rivestem, produkuje 128 bitovy vystup, iterace ve trech cyklech
publikovan utok proti prvnim dvoum cyklum algoritmu
autor provedl vylepseni MD5

MD5 pracuje nad vstupnimi bloky delky 512 bitu, 128 bitovy vystup, pracuje ve ctyrech cyklech
velmi komplikovany vypocet zahrnujici bitove logicke operace, posuny, scitani

Navrhy MAC funkci

obecna struktura stejna jako MDC, funkce f a pripadne i IV zavisi navic na klici K
existuje velmi male mnozstvi algoritmu

nejcasteji pouzivanou metodou je pocitani DES nebo podobneho algoritmu v modu CBC, resp CFB, konkretni schemata se lisi volbou pripadne kombinaci zminenych modu, pouzitim ruznych zarovnani...;

Jinou moznosti je vypocet

f = E(K, X_i H_i-1) xor

X_i

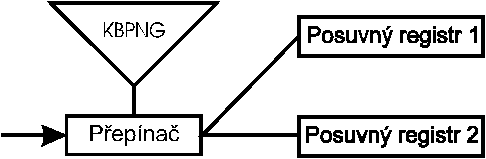
Stream MAC

potrebujeme kryptograficky bezpecny generator pseudonahodnych sekvenci
podle vysledku generatoru je vstupni bit presunut do prvniho nebo druheho posuvneho registru, vysledek urcen konecnym obsahem posuvnych registru

Jeden z generatoru

Generatory nahodnych sekvenci

Kongruencni generator

Linearni X_i = (aX_i-1+b) mod m

pri vhodne volbe a, b, m (napr. m prvocislo) generuje neopakujici se posloupnost delky m - generator s maximalni delkou

Kvadraticky X_i = (aX²_i-1+bX_i-1+c) mod m

Kubicky X_i = (aX³_i-1+bX²_i-1+cX_i-1+d) mod m

kongruencni generatory jsou velmi rychle, avsak predikovatelne, byla vypracovana analyza

Posuvne registry s linearni zpetnou vazbou

(linear feedback shift registers)

sestavaji z posuvneho registru a vypousteci sekvence (tap sequence), coz je polynom stupne max. delky posuvneho registru

v kazdem kroku je obsah registru posunut o bit doprava, vystupem je nejpravejsi bit, registr se zleva doplni o XOR tech bitu v registru, ktere odpovidaji koeficientum vypousteciho polynomu

pro generator s maximalni delkou je nutno volit primitivni polynom stupne n - ireducibilni polynom delici x^2ⁿ-1 + 1, ktery nedeli x^d + 1 pro lib d delici 2ⁿ - 1

Blum-Micali

X_i = a^X_i-1

a, p prvocisla, bezpecnost plyne z obtiznosti vypoctu diskretniho logaritmu

Stridajici stop-and-go generator

pouziva tri posuvne registry s linearni zpetnou vazbou

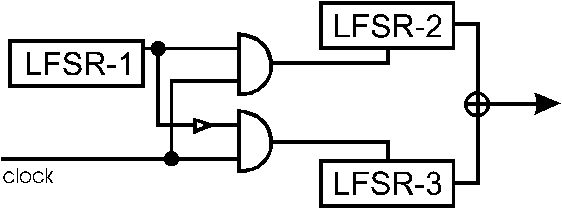
Schema stridajiciho generatoru

impuls hodin jsou v zavislosti na hodnote LFSR-1 priveden na LFSR-2 nebo LFSR3, vystup techto registru je XORovan, cimz vznika vysledna hodnota.

gnerator ma velmi dlouhou periodu

RSA generator

X_i = X^e_i-1 mod n

vysledkem nejnizsi bit X_i. Bezpecnost ekvivalentni s bezpecnosti RSA

Blum Blum Shub

X_i = X²_i-1 mod n kde n je Blumovo cislo - soucin dvou velkych prvocisel kongruentnich s 3 mod 4. Generator se inicializuje hodnotou X₀ = X² mod n, kde X je nahodne cislo nesoudelne s n.

Vysledkem je nejnizsi bit X_i . Bezpecnost vyplyva z obtiznosti faktorizace velkych cisel. Generator je nepredikovatelny vlevo i vpravo, ale je mozne se znalosti faktoru p, q cisla n spocitat primo libovolne prvek generovane posloupnosti!

X_i = X₀^{(2ⁱ) mod ((p-1)(q-1))} mod n

Dosud neni znama metoda zlomeni tohoto generatoru. Nevyhodou je znacna pomalost.

Tuto stranku shledlo jiz

zvedavcu ...