Prednášajúci: Prof. V. Kvasnička a Doc. J. Pospíchal {kvasnic@cvt.stuba.sk}

Katedra matematiky CHTF STU,

Semester: zimný

Rozsah: 2-0-0

1. Základné pojmy evolučných algoritmov – optimalizačný problém a jeho kódovanie, binárna reprezentácia reálnej premennej, transformácia spojitého optimalizačného problému na binárny optimalizačný problém.
2. Horolezecké (hill climbing) algoritmy – elementárne stochastické optimalizačné algoritmy, slepý algoritmus a horolezecký algoritmus, horolezecký algoritmus s učením, metóda zakázaného hľadania (tabu search), evolučné programovanie.
3. Genetický algoritmus – darvinovská evolúcia v živej prírode, základné pojmy, populácia a sila (fitness) chromozómov, kríženie chromozómov, implementácia genetického algoritmu, teória genetického algoritmu, Hammingova bariéra, ”messy” chromozómy, paralelná implementácia genetického algoritmu.
4. Genetické programovanie – základné pojmy z teórie grafov, koreňové stromy a Readov kód, symbolická regresia, rekonštrukcia stromov s požadovanými vlastnosťami, kódovanie funkcií pomocou acyklických orientovaných grafov.
5. Simulované žíhanie – základné pojmy, vzťah k štatistickej fyzike, paralelná implementácia.
6. Kombinatoriálne optimalizačné problémy – klasifikácia, základné úlohy z teórie grafov a operačného výskumu, špecifikácie operátorov mutácie a kríženia pre kombinatoriálne optimalizačné problémy.
7. Evolučné stratégie – historické poznámky, stratégia (1+1) - jeden rodič a jeden potomok, distribúcia pravdepodobnosti, generovanie náhodných čísel, viacčlenné stratégie a kovariancie, súvislosti s evolučným programovaním.
8. Neurónové siete – klasifikácia neurónových sietí, neurónové siete s dopredným šírením, rekurentné neurónové siete, parametrická adaptácia neurónových sietí pomocou gradientovej optimalizačnej metódy, adaptácia neurónových sietí ako stochastický optimalizačný problém, štrukturálna adaptácia neurónových sietí pomocou evolučných algoritmov.
9. Umelý život – definície života a umelého života, umelá inteligencia a multiagentové systémy, kognitívne aparáty agentov, darvinovská evolúcia multiagentových systémov, emergencia kooperatívnych vlastnosti. Celulárne automaty, evolúcia pravidiel, vznik komplexných javov. Kooperácia, súťaženie, altruizmus, dilema väzňov a tragédia spoločného. Emergencia zložitosti, vznik života evolúciou neživého.
10. DNA výpočty – základné pojmy z molekulovej biológie, štruktúra a vlastnosti DNA, teoretické modely výpočtového procesu, experiment L. Adlemana s hľadaním hamiltónovskej cesty v orientovanom grafe pomocou DNA, DNA počítače in vivo.

Literatúra:

1. V. Kvasnička, J.Pospíchal a P. Tiňo: Evolučné algoritmy, STU Bratislava 2000..
2. T. Bäck: Evolutionary Algorithms in Theory and Practice - Evolutionary Strategies, Evolutionary Programming, Genetic Algorithms. Oxford University Press, Oxford, UK, 1996.
3. Z. Michaliewicz: Genetic Algorithms + Data Structures = Evolution Programs. Springer Verlag, Berlin, 1992.
4. W. Banzhaf, P. Nordin, R. E. Keller, and F. D. Francone: Genetic Programming – An Introduction. Morgan Kaufmann Publishers, San Francisco, 1998.

Charles Darwin "On the Origin of Species" (doc)

http://www.mkp.com/books_catalog/1-55860-605-x.asp

text kapitoly pdf.

Tutoriál od Prof. Hans-Paul Schwefel "On Natural Life's Tricks to Survive and Evolve"

(pdf alebo ps.zip)

Tutorial od Prof. John Koza (University of Stanford) "Genetic Programming: Biologically Inspired Computation that Creatively Solves Non-Trivial Problems" (pdf)

 Tutorial od Prof. Darrell Whitley "A Genetic Algorithm Tutorial" (pdf)

Kapitola 1- Úvodné poznámky (ps.zip alebo pdf)

Kapitola 2 - Základné pojmy evolučných algoritmov (ps.zip alebo pdf)

Kapitola 3 - Horolezecké algoritmy (ps.zip alebo pdf)

Kapitola 4 - Genetické algoritmy (ps.zip alebo pdf)

Kapitola 5 - Genetické programovanie (ps.zip alebo pdf)

Kapitola 6 - Simulované žíhanie (ps.zip alebo pdf)

Kapitola 7 - Kombinatoriálne optimalizačné problémy (ps.zip alebo pdf)

Kapitola 8 - Evolučné stratégie (ps.zip alebo pdf)

Kapitola 9 - Umelý život (ps.zip alebo pdf)

Kapitola 10 - Neurónové siete (ps.zip alebo pdf)

 Všeobecné predstavy o darvinovskej evolúcii, chápanie evolúcie ako algoritmu, význam učenia v evolúcii (Baldwinov efekt), mémy (Dawkins) ako nosič informácie pre chromozómy.

Priesvitky k prednáške (ps.zip alebo pdf)

Pozri tiež pripravovaný článok "Umelá evolúcia" (ps.zip alebo pdf)

 Binárne kódovanie reálnej premenne, transformácia spojitého optimalizačného problému na binárny optimalizačný problém. Slepý algoritmus, horolezecký algoritmus (hill climbing), horolezecký algoritmus a učením, metóda zakázaného prehľadávania (tabo search), evolučné programovanie. Predmet tejto prednášky odpovedá 2. a 3. kapitole knihy "Evolučné algoritmy".

Priesvitky k prednáške (ps.zip alebo pdf)

 Genetické algoritmy, "messy" genetický algoritmus, paralélny genetický algoritmus. Základné princípy genetických algoritmov.

Priesvitky k prednáške (ps.zip alebo pdf)

 Teória genetických algoritmov.

Priesvitky k prednáške (ps.zip alebo pdf)

Genetické programovanie, symbolická regresia.

Priesvitky k prednáške (ps.zip alebo pdf)

Priesvitky k prednáške (ps.zip alebo pdf)

Priesvitky k prednáške (ps.zip alebo pdf)

Priesvitky k prednáške (ps.zip alebo pdf)

Priesvitky k prednáške (ps.zip alebo pdf)

Neurónové siete.

Priesvitky k prednáške (ps.zip alebo pdf)

Priesvitky k prednáške (ps.zip alebo pdf)

Podrobnosti o skúške, témy "case studies" (ps.zip alebo pdf)

 Skúška - témy "case studies"

Skúška z prednášky "Evolučné algoritmy" bude udelená na základe vypracovanej "case study" z oblastí uvedených nižšie. "Case study" je písomná práca v rozsahu približne 7-10 strán (page size A4, font size 10, line spacing single, obsahuje meno autora a jeho internetovské koordináty), obsahuje teoretický popis použitej metódy a získané numerické výsledky, ktoré sú ilustrované tabuľkami a grafmi. Integrálnou prílohou "case study" bude aj fungujúci program, pomocou ktorého bola vypracovaná jej aplikačná časť.

Skúška sa uskutoční na Katedre matematiky CHTF STU vždy v piatok v intervale od 9-11 hod., na skúšku je potrebné sa prihlásiť na t.č. 59325296 alebo emailom {kvasnic,pospich}@cvt.stuba.sk

 Upozornenie: Záujemci o skúšku FTP uploadujú aspoň jeden deň pred konaním skúšky (do 16.00 hod.) vypracovanú "case study" na adresu

ftp://math.chtf.stuba.sk/received/vlado

Ako vytvoriť PS dokument pomocou MS WORD-u: Priradí sa poscriptovská tlačiareň a nechá sa tlačiť do súboru (print to file), takto vznikne PS súbor, je potrebné ho ešte prekontrolovať pomocou GhostView, či sa vytvoril korektne.

Téma 1. Horolezecký algoritmus pre funkciu f(x) definovanú v

pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokúste sa optimalizovať parametre c₀ a P_mut tak, aby ste skoro so 100% istotou dostali globálne minimum s čo najmenším počtom iteračných krokov.

(tému vypracuje Jaroslav Ondriska, skúška 12. 1. 2001) 

Téma 2. Metóda zakázaného hľadania aplikovaná na TSP (riešenie obchodného cestujúceho), pričom cesta nech je vyjadrená pomocou permutácie. Transformačné operátory tÎ S sú realizované ako permutácie transpozícií dvoch objektov. Operátor t_ij pôsobí na permutáciu P ako transpozícia objektov i a j,

pre i<j. Ako testovací príklad použite ortogonálnu mriežku bodov - miest, kde sa vzdialenosť počíta pomocou Hammingovej metriky (pozri príklad 8.2). Pokúste sa o optimalizáciu veľkosti "s" zakázaného zoznamu T (tabu listu) a maximálneho počtu iterácií time_max pre rôzne hodnoty N dimenzie ortogonálnej mriežky bodov, N=4,5,...,10, tak , aby ste s 95% pravdepodobnosťou dostali korektný výsledok. Podobné úvahy vykonajte aj pre suboptimálne výsledky, ktoré sa líšia len niekoľko málo jednotiek od optimálneho výsledku.

(tému vypracuje Branislav Květoň, termín skúšky 9. 2. 2001) 

Téma 3. Použite ANT colony optimalizáciu pre TSP (problém obchodného cestujúceho) urobenú na základe článku ftp://iridia.ulb.ac.be/pub/mdorigo/journals/IJ.15-BIOSYS97.pdf
pre optimalizáciu náhodne rozmiestnených miest vo štvorci, pravidelne rozmiestnených miest na štvorcovej mriežke a štandardných problémov TSP použitých v článku. Zobrazte závislosť priemerne dosiahnutej najmenšej dĺžky cesty 1) na parametru b , ktorý vyjadruje váhu feromónovej stopy v porovnaní s momentálnou dĺžkou hrany 2) na parametru rýchlosti učenia a a 3) na parametru t ₀ a konečne 4) na funkcii t (r,u) vyjadrenej v článku ako inverzia dĺžky hrany r,u - študujte iné spôsoby prepočtu tejto dĺžky hrany, pričom sa môžete inšpirovať rôznymi spôsobmi prepočtu účelovej funkcie chromozómu na silu.

(tému vypracuje Juraj Frivolt, termín skúšky 5. 3. 2001) 

Téma 4. Porovnajte účinnosť zakódovaní riešení genetického algoritmu pre TSP (úlohu obchodného cestujúceho), kde mestá sú na pravouhlej mriežke a zakódovanie je

1. klasická permutácia
2. pri stálom štartovacom bode pri strede mriežky budú jednotlivé vstupy chromozómu čísla od 1 do 3, ktoré značia poradie ďaľšej cesty z daného bodu pri počítaní zľava od vstupnej cesty (teda 1=vľavo, 2=rovno, 3 vpravo). Pokiaľ sa algoritmus dostane "nožičkou" Téčka na hranu, 2 znamená napravo a 3 návrat naspäť. Chromozóm bude mať dĺžku odpovedajúcu ideálnemu riešeniu, funkčná hodnota riešenia bude zostavená z členu určujúceho počet navštívených miest spolu s inverziou vzdialenosti posledného mesta od východzieho.

(tému vypracuje Martin Kanich, termín skúšky 9. 2. 2001) 

Téma 5. Generujte magické štvorce pomocou genetického algoritmu. ``Magický štvorec'' rádu n je n´ n matice obsahujúca všetky celé čísla od 1 po n*n, každé z nich práve raz, tak, že súčty všetkých riadkov, stĺpcov a diagonál sú tie isté. Inými slovami, je to permutácia čísel 1 po n*n, usporiadaná do pravouhlej mriežky, s vlastnosťou že každý súčet riadku, stĺpca, alebo diagonály matice sa rovná tomu istému celému číslu.

Napríklad, magický štvorec rádu 3 je

    2  7  6
    9  5  1
    4  3  8

3 sumy riadkov, tri stĺpcov a dve diagonálne sumy sú 15.

(Úloha odpísaná z http://king.mcs.drexel.edu/~shartley/MCS770/ProgAssgns/third.html)

(tému vypracuje Daniel Ferák, na skúška prihlásený 10.1.2001) 

Téma 6. Problém všeobecnej splniteľnosti (general satisfiability SAT), aj keď zahŕňame všetky druhy logických klauzúl, nie len konjunkcie a disjunkcie. Každý problém pozostáva z 20 boolovských premenných (A0 - A19) a a sady obmedzení. Cieľom je samozrejme nájsť pravdivostné priradenie ku každej premennej tak, že sú splnené všetky obmedzenia. V uvedených problémoch sú najlepšie riešenia pre človeka triviálne, ale GA nemá našu znalosť logiky a musí prehľadávať extenzívne. Pre každý z GA behov vykreslite graf sily(min,max a priemer).

A) 5 konjunkcií, obmedzenia sú

(A0 and A1 and A2 and A3)

(A4 and A5 and A6 and A7)

(A8 and A9 and A10 and A11)

(A12 and A13 and A14 and A15)

(A16 and A17 and A18 and A19)

1. Popíšte vašu reprezentáciu a funkciu sily. Pri vašej reprezentácii, ako veľký je priestor prehľadávania?
2. Opíšte rozdiely v správaní GA keď použijete veľkosť populácie 100 alebo 20. Pri každom z prípadov použite 50 generácií, pravdepodobnosť mutácie (pmut) 0.01 na chromozóm (nie na gén) a pravdepodobnosť kríženia (pcross) 0.75.

c) Použite veľkosť populácie 50, 50 generácií, pmut = 0.01 a 3 rozdielne pravdepodobnosti kríženia: 0.1, 0.3 and 0.8. V čom sa líši správanie algoritmu pre dané 3 behy?

3. Pri vašej funkcii sily, je povrch fitness hladký alebo rozoklaný? Vysvetlite Váš náhľad na vec. Keď vidíte povrch ako hladký (rozoklaný), ako by ste zmenili fitness funkciu aby bola viac rozoklaná (hladká )?

B) 10 konjunkcií, obmedzenia sú

(A0 and A1) (A2 and A3)

(A4 and A5) (A6 and A7)

(A8 and A9) (A10 and A11)

(A12 and A13) (A14 and A15)

(A16 and A17) (A18 and A19)

e) Zbehnite tento problém za rovnakých podmienok ako pri a, s rovnakou fitness funkciou. Aké sú rozdiely? Prečo sa objavili rozdiely, aj keď obmedzenia sú logicky ekvivalentné? Môžete pomocou použitej fitness funkcie vysvetliť rozdiel?

g) Vymyslite novú fitness funkciu podstatne rozdielnu od prvej a testujte ju pre a) a e) s populáciou veľkosti 100, 100 generáciách, pcross = 0.8, pmut: 0.01. Aké sú výsledky v porovnaní s prvou fitness funkciou? Ako sa zmenil "povrch"?

B) 7 disjunkcií, 4 konjunkcie, obmedzenia sú

(A0 or A1 or A2 or A3)

(not(A0) or not (A1))

(not(A0) or not(A2))

(not(A0) or not(A3))

(not(A1) or not(A2))

(not(A1) or not(A3))

(not(A2) or not(A3))

(A4 and A5 and A6 and A7)

(A8 and A9 and A10 and A11)

(A12 and A13 and A14 and A15)

(A16 and A17 and A18 and A19)

h) Testujte s populáciou veľkosti 100, 100 generáciách, pcross = 0.8, pmut: 0.1. s obidvoma Vámi navrhnutými fitness funkciami, vysvetlite rozdiely v správaní.

(Úloha odpísaná z http://www.ifi.ntnu.no/~keithd/classes/mnfit378/homework/2000/assign1.html)

(tému vypracuje Miroslav Zervan) 

Téma 7. Riadenie robota

	(s v v v j j)

	######
	#   x#
	### ##
	#e  R#
	######

(Úloha odpísaná z http://www.indiana.edu/~gasser/Q351/ga-robot.ss)

(tému vypracuje Pavol Palka, poslal case-study, termín skúšky zatiaľ neurčený) 

Téma 8. Použite simulované žíhanie pre riešenie pohybu koňa na šachovnici, kde zo zadaného poľa máte prebehnúť všetky ostatné poľa, pričom na každé pole vstúpite iba raz. Ako druhú časť úlohy riešte rovnaký problém s podmienkou, že sa kôň musí vrátiť naspäť. Pri riešení použite perturbáciu (mutáciu) toho druhu, že počiatok postupnosti polí do náhodne vybraného počtu polí skopírujete do nového riešenia a zvyšok vygenerujete. Úloha sa dá riešiť aj spätným prehľadávaním, ale len pre malé prípady.

(tému vypracuje Slavomír Ondko) 

Téma 9. Zhodnoťte vplyv stratégií výberu na optimalizáciu pri použití definícií z

http://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html

pre prepočítanie sily proporčne (viď formula 4.11c v knihe Evolučné algoritmy) alebo na základe usporiadania podľa veľkosti (formula 4.12b) a vlastný výber ruletou, turnajom, pomocou tzv. stochastic universal sampling, local selection, výber odrezaním najhorších (truncation selection) opísaných v

http://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html

(zobraté z http://www.aridolan.com/ga/gaa/gaa.html)

Ackleyho funkcia

f(x) = 20+e-20*exp(-0.2*exp(sqrt((1/n)*sum(x(i)^2))-exp((1/n)*sum(cos(2*Pi*x(i)))

Rosenbrockova funkcia

f(x) = sum(100*(x(i)-x(i-1)^2)^2 + (1-x(i-1))^2

Schwefelova funkcia

f(x) = 418.9829*n + sum(-x(i)*sin(sqrt(abs(x(i))))

Rastriginova funkcia

f(x) = 10.0*n + sum(x(i)^2 - 10.0*cos(2*Pi*x(i)))

Griewankova funkcia

f(x) = 1/4000*sum(x(i)-100)^2 - prod((x(i)-100)/sqrt(i)) + 1

Sférický model

f(x) = sum((x(i)-1)^2)

Funkcie jednej premennej

f(x) = x^4 - 12*x^3 + 15*x^2 + 56*x - 60

minimalizácia funkcie viac premenných

f(x1,x2,x3,x4,x5) = x1*sin(x1) + 1.7*x2*sin(x1) - 1.5*x3 - 0.1*x4*cos(x4+x5-x1) + (0.2*x5^2-x2) - 1

(x1*x2*x3*x4*x5)/(x6*x7*x8*x9*x10) kde (x1..x10)=[1..10]

(tému vypracuje ...) 

Téma 10. Zhodnoťte vplyv kríženia a mutácie pri optimalizácii pri použití definícií z

http://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html

pre kríženie reálnych hodnôt: lineárnou kombináciou, priemerom, diskrétne a binárnych hodnôt: jednobodové, dvojbodové, viacbodové, uniformné a mutáciu binárnych premenných a reálnych premenných (z evolučných stratégií) pre funkcie daných v príklade 9.

(tému vypracuje ...) 

pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokuste sa nájsť minimálnu veľkosť populácie a také hodnoty pravdepodobností P_cross a P_mut, aby ste skoro so 100% istotou dostali globálne minimum s predpísaným minimálnym počtom krokov.

(tému vypracuje Tomáš Kaláb, termín skúšky je 9. 2. 2001) 

Téma 12. Genetický algoritmus pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke. Použite oba prístupy na kódovanie cesty, tak priamo pomocou permutácie, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.

(tému vypracuje Fridrich Matz, termín skúšky je 28. 5. 2001) 

Téma 13. Genetický algoritmus pre úlohu Number Partitioning Problem. Použite oba prístupy na kódovanie zobrazenia p , tak priamo pomocou N-tice celých čísel, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.

 (tému vypracuje Andrej Kružic) 

Téma 14. L-systém (tvorba "kríka") je daný nasledovnými pravidlami: (1) štartovný bod F, (2) produkčné pravidlo F ® F [+F][-F], kde F znamená "nakresli čiaru" (začíname kolmou čiarou z počiatočného bodu so súradnicami 0,0 do koncového bodu so súradnicami 0,10). Symbol [ znamená zapamätať si súradnice koncového bodu a zodpovedajúcu zmenu súradníc

dx= x koncový - x počiatočný , dy= y koncový - y počiatočný

x koncový = x počiatočný + 0.7 (cos(40^o) dx - sin(40^o) dy)

y koncový = y počiatočný + 0.7 (sin(40^o) dx + cos(40^o) dy)

Symbol - znamená otočiť sa doprava (použili sme prepis pre súradnice nového bodu

x koncový = x počiatočný + 0.7 (cos(33^o) dx + sin(33^o) dy)

y koncový = y počiatočný + 0.7 (sin(33^o) dx - cos(33^o) dy)

Vytvorte obrázok trojrozmerného stromčeka, kde jednotlivé vetvy sa nebudú skracovať faktorom 0.7, ale náhodným číslom s gaussovským rozložením pravdepodobnosti so stredom napr. v 0.7, kde aj hrúbka kmeňa sa bude zmenšovať a bližšie vetvy budú vyzerať hrubšie, kde uhly vetiev v priestore tiež budú dané náhodne. Vyskúšajte aj iné produkčné systémy, napr. počet vetiev bude daný náhodným číslom od 2 do 3.

(tému vypracuje Peter Novák, poslal case-study, termín skúšky zatiaľ neurčený) 

Téma 15. Namodelujte priebehy množstva dravcov a koristi ukázané v nasledujúcich obrázkoch podľa rovníc

dN₁(t)/dt = N₁(r_1- b₁N₂ )

dN₂(t)/dt = N₂(- r₂+b₂N₁

kde N₁(t) je počet kusov koristi (alebo hostiteľa) a N₂(t) je počet kusov dravcov (alebo parazitov) v čase t. Predpokladáme, že za neprítomnosti dravcov sa korisť rozmnožuje rýchlosťou r₁, zatiaľ čo za absencie koristi dravci hynú rýchlosťou r₂. Nech b₁ zodpovedá schopnosti dravcov požierať korisť a b₂ vplyvu množstva koristi (a teda nasýtenia dravcov) na ich rozmnožovanie. Nech r₁= 1.5, b₁=0.1 r₂= 0.25 b₂= 0.01 a N₁(0)= 15 a N₂(0)=20. Znázornite priebeh, nie však pomocou klasického riešenia pomocou diferenciálnych rovníc, ale vytvorením stochastického modelu, kde množstvá dravcov a koristi a ich prírastky/úbytky budú dané celými číslami; v prípade, že zmena nie je vyjadrená celým číslom, berte neceločíselnú časť ako pravdepodobnosť a rozhodnite o zaokrúhlení nahor/nadol na základe porovnania tejto pravdepodobnosti s náhodným číslom z intervalu (0,1) – použite analógiu algoritmov 10.1 a 10.2 z kapitoly o umelom živote. Numericky modelujte a diskutujte pravdepodobnosť zániku jedného či obidvoch druhov v závislosti na počiatočných množstvách jedincov a na ostatných parametroch.

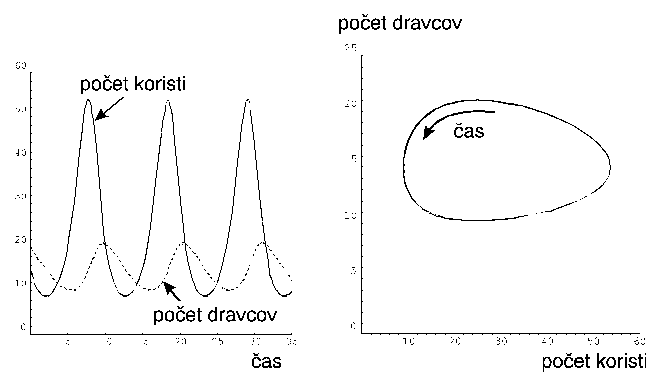
Prvá závislosť ukazuje oscilácie počtu dravcov a množstva koristi v čase, druhý obrázok je trajektóriou sústavy diferenciálnych rovníc (10.4).

(tému vypracuje Michaela Ačová) 

Téma 16. Vytvorte program pre animáciu pohybu žubrienok (pozri priložený obrázok), kde veľký kruh je prekážka, "hlavička žubrienok" predstavuje umiestnenie žubrienky v dvojrozmernom priestore a dĺžka a smer chvostíka určujú rýchlosť a smer pohybu žubrienky. Počítačový model sa má riadiť troma základnými vlastnosťami:

(tému vypracuje Vladimír Držík, na skúšku prihlásený 5.1.2001) 

Téma 17. Použitie ANT COLONY optimalizácie na hľadanie najkratšej cesty v bludisku,
riešené paralelným behom niekoľkých "mravcov" v bludisku na
základe zadefinovaných vlastností správania mravcov ako sú popísané v
článku M. Doriga: ftp://iridia.ulb.ac.be/pub/mdorigo/journals/IJ.10-SMC96.pdf Rozobratie rôznych prístupov k zanechávaniu a vyhodnocovaniu feromónovych stop pri riešení tohto problému.

(tému vypracuje Vladimír Škopek, skúška dňa 2. 2. 2001) 

1. Vladimír Držík: Simulácia pohybu žubrienok (case study ps.zip a pdf, implemetacia exe.zip)
2. Daniel Ferák: Generovanie magických štvorcov pomocou GA (pôvodná verzia - case study doc.zip, ps.zip a pdf.zip, implemetacia zip, opravená verzia - case study doc.zip, ps.zip a pdf.zip, impementácia zip )
3. Jaroslav Ondriska: Horolezecký algoritmus pre reálnu funkciu jednej premennej (case study doc.zip, ps.zip a pdf.zip, impementácia zip)
4. Peter Novák: L_systém - tvorba kríka (case study pdf, implementácia exe.zip)
5. Pavol Palka: Riadenie robota (case study ps.zip, pdf.zip, bludisko zip, implemetácia exe.zip)
6. Vladimír Škopek: Použitie ANT COLONY optimalizácie na hľadanie najkratšej cesty v bludisku (case study doc.zip, ps.zip, pdf.zip, implementácia exe.zip)
7. Branislav Květoň: Metóda zakázaného hľadania aplikovaná na TSP (case study doc.zip, ps.zip, pdf, source.zip, implementácia exe.zip)
8. Tomáš Kaláb: Použitie GA pre hľadanie globálneho minima funkcie jednej premennej (case study ps.zip, pdf, implementácia exe.zip)
9. Martin Kanich: Porovnajte účinnosť zakódovaní riešení genetického algoritmu pre TSP (case study doc.zip, ps.zip, pdf, source1.zip, source2.zip , implementácia exe.zip )
10. Juraj Frivolt: Riešenie problému obchodného cestujúceho pomocou kolónii mravcov (case study doc.zip, ps.zip, pdf, source.zip).
11. Fridrich Matz: Genetický algoritmus pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke (case study ps.zip, pdf.zip implementácia exe )

 viď http://math.chtf.stuba.sk/evol/prednaska99.htm naspodku strany