Prednáška "Evolučné algoritmy"
MFF UK, 4. ročník, odbor "informatika"
Šk.r. 2001/02, semester zimný
Dátum prednášky:
utorok o 11.30 hod, poslucháreň V
Sylabus prednášky:
Prednášajúci: Prof. V. Kvasnička {kvasnic@cvt.stuba.sk}a Doc. J. Pospíchal {pospich@cvt.stuba.sk}
Katedra matematiky CHTF STU,
Semester: zimný
Rozsah: 2-0-0
Literatúra:
Charles Darwin "On the Origin of Species" (
doc)
Úvodná kapitola z knihy "
Evolutionary Design by Computers", editor Peter J. BentleyISBN 1-55860-605-X, domovská stránka knihy je na adrese
http://www.mkp.com/books_catalog/1-55860-605-x.asp
text kapitoly
pdf.
Tutoriál od Prof.
Hans-Paul Schwefel "On Natural Life's Tricks to Survive and Evolve"(
pdf alebo ps.zip)
Tutorial od Prof. John Koza (University of Stanford) "Genetic Programming: Biologically Inspired Computation that Creatively Solves Non-Trivial Problems" (pdf)
Tutorial od Prof. Darrell Whitley "A Genetic Algorithm Tutorial" (pdf)
Predbežné texty ku knihe "Evolučné algoritmy"
Jednotlivé kapitoly môžu slúžiť ako základný text prednášky, kde sú uvedené aj príklady na precvičenie.
Obsah
Kapitola 1- Úvodné poznámky (
ps.zip alebo pdf)Kapitola 2 - Základné pojmy evolučných algoritmov (
ps.zip alebo pdf)Kapitola 3 - Horolezecké algoritmy (
ps.zip alebo pdf)Kapitola 4 - Genetické algoritmy (
ps.zip alebo pdf)Kapitola 5 - Genetické programovanie (
ps.zip alebo pdf)Kapitola 6 - Simulované žíhanie (
ps.zip alebo pdf)Kapitola 7 - Kombinatoriálne optimalizačné problémy (
ps.zip alebo pdf)Kapitola 8 - Evolučné stratégie (
ps.zip alebo pdf)Kapitola 9 - Umelý život (
ps.zip alebo pdf)Kapitola 10 - Neurónové siete (
ps.zip alebo pdf)
1. prednáška
Všeobecné predstavy o darvinovskej evolúcii, chápanie evolúcie ako algoritmu, význam učenia v evolúcii (Baldwinov efekt), mémy (Dawkins) ako nosič informácie pre chromozómy.
Priesvitky k prednáške (ps.zip alebo pdf)
Pozri tiež pripravovaný článok "Umelá evolúcia" (
ps.zip alebo pdf)
2. prednáška
Binárne kódovanie reálnej premenne, transformácia spojitého optimalizačného problému na binárny optimalizačný problém. Slepý algoritmus, horolezecký algoritmus (hill climbing), horolezecký algoritmus a učením, metóda zakázaného prehľadávania (tabo search), evolučné programovanie. Predmet tejto prednášky odpovedá 2. a 3. kapitole knihy "Evolučné algoritmy".
Priesvitky k prednáške (ps.zip alebo pdf)
3. prednáška
Genetické algoritmy, "messy" genetický algoritmus, paralélny genetický algoritmus. Základné princípy genetických algoritmov.
Priesvitky k prednáške (ps.zip alebo pdf)
4. prednáška
Teória genetických algoritmov.
Priesvitky k prednáške (ps.zip alebo pdf)
5. prednáška
Genetické programovanie, symbolická regresia.
Priesvitky k prednáške (ps.zip alebo pdf)
6. prednáška
Simulované žíhanie.
Priesvitky k prednáške (ps.zip alebo pdf)
7. prednáška
Kombinatoriálne optimalizačné problémy. Úloha obchodného cestujúceho, Number Partitioning Problem.
Priesvitky k prednáške (ps.zip alebo pdf)
8. prednáška
Evolučné stratégie.
Priesvitky k prednáške (ps.zip alebo pdf)
9. prednáška
Umelý život.
Priesvitky k prednáške (ps.zip alebo pdf)
10. prednáška
Neurónové siete.
Priesvitky k prednáške (ps.zip alebo pdf)
11. prednáška
Swarm výpočty.
Priesvitky k prednáške (ps.zip alebo pdf)
12. prednáška
Podrobnosti o skúške, témy "case studies" (ps.zip alebo pdf)
Skúška - témy "case studies"
Skúška z prednášky "Evolučné algoritmy" bude udelená na základe vypracovanej "case study" z oblastí uvedených nižšie. "Case study" je písomná práca v rozsahu približne 7-10 strán (page size A4, font size 10, line spacing single, obsahuje meno autora a jeh
o internetovské koordináty), obsahuje teoretický popis použitej metódy a získané numerické výsledky, ktoré sú ilustrované tabuľkami a grafmi. Integrálnou prílohou "case study" bude aj fungujúci program, pomocou ktorého bola vypracovaná jej aplikačná časť.Skúška sa uskutoční na Katedre matematiky CHTF STU vždy v piatok v intervale od 9-11 hod., na skúšku je potrebné sa prihlásiť na t.č. Telefón: (+421 2) 5249 5177, (+421 2) 5932 5104, alebo emailom {kvasnic,pospich}@cvt.stuba.sk
Každá téma z "case study" bude môcť byť použitá iba jedným študentom, na tému sa treba prihlásiť a postupné "prideľovanie" bude prebiehať podľa pravidla “kto skôr príde..”. Podstatou skúšky bude diskusia o riešenej úlohe a taktiež všeobecné vedomosti z evolučných algoritmov.
Upozornenie: Záujemci o skúšku pošlú e-mailom aspoň jeden deň pred konaním skúšky ako attachment (do 16.00 hod.) vypracovanú "case study" na adresy {kvasnic,pospich}@cvt.stuba.sk , a musia sa uistiť, že sme ich súbor dostali v poriadku (pozor, musí byť do 2 MB), alebo sa dohodnú na inom spôsobe dodania súboru. Súbor má byť v PS alebo v PDF formáte, pričom "čitateľnosť" súborov nech je prekontrolovaná pomocou GhostView-u alebo AcrobatReader-u. Práce budú vystavené na tejto stránke pre poučenie budúcich generácií.
Ako vytvoriť PS dokument pomocou MS WORD-u
: Priradí sa poscriptovská tlačiareň a nechá sa tlačiť do súboru (print to file), takto vznikne PS súbor, je potrebné ho ešte prekontrolovať pomocou GhostView, či sa vytvoril korektne.
Pakovanie je klasickým problémom v optimalizáci
i. Predpokladajme, že máme nákladný voz schopný uviezť akýkoľvek počet krabíc, pokiaľ ich celková váha neprekročí W. V skladisku máte nelimitované množstvo rozličných typov tovaru. Každý typ položky i má váhu wi a hodnotu vi . Váš problém je určiť, ktorou kombináciou objektov dosiahnete najvyššiu hodnotu bez prekročenia maximálnej povolenej celkovej váhy. Napríklad, keď váhy a hodnoty sú|
Položka |
váha |
hodnota |
|
|
pomaranče |
3 |
5 |
|
|
knihy |
8 |
11 |
|
potom náklaďák s maximálnou nosnosťou W=200 môže viezť:
|
pomaranče |
knihy |
váha |
hodnota |
|
30 |
13 |
194 |
293 |
|
40 |
10 |
200 |
310 |
|
50 |
6 |
198 |
316 |
|
60 |
2 |
196 |
322 |
Najlepšia stratégia je naložiť toľko krabíc s pomarančmi ako sa len dá a zvyšok zaplniť knihami. Vyriešte problém pre väčší počet položiek s náhodne definovanými hodnotami a váhami pomocou genetického algoritmu, s obmedzeným počtom niektorých položiek, vymyslite si vlastnú reprezentáciu problému a k nej odpovedajúce chromozómy, mutácie a kríženie,
porovnajte váš algoritmus s kanonickým genetickým algoritmom, a použite pokutovaciu funkciu. (Adaptované z http://www.epcc.ed.ac.uk/epic/ga/intro.html)(tému vypracuje Jan Marčok, Jan.Marcok@st.fmph.uniba.sk)
Rozvrhovací problém je intenzívne v
oblasti operačného výskumu už veľa rokov. Jednou z formulácií problému je predpokladať, že máme množinu N úkolov ti, i=1..N, každý z nich vyžaduje niektoré zo zdrojov rj po zadaný čas timei,rj. Našou úlohou je nájsť najrýchlejší rozvrh pre celkové splnenie týchto úkolov, pričom zdroje môžu byť využívané súčasne, ale každý zdroj iným úkolom. Na poradí zdrojov pre úkol nezáleží. Vyriešte problém pre väčší počet úkolov s náhodne definovanými požadovanými zdrojmi a časmi pomocou genetického algoritmu, vymyslite si vlastnú reprezentáciu problému a k nej odpovedajúce chromozómy, mutácie a kríženie, porovnajte váš algoritmus s kanonickým genetickým algoritmom. Použite pokutovaciu funkciu pri nesplnení ohraničení.(
tému vypracuje Ján Wall, 8wall@nw.fmph.uniba.sk)
Téma 3.
Porovnanie genetického algoritmu zo simplexovou metódouOptimalizujte funkciu f(x,y)=cos2(n Pi x) exp(-r2 / s2), r2=(x-0.5)2+(y-0.5)2 pre x,yÎ [0,1], kde n=9 a s2=0.15. Nájdite globálne maximum tejto funkcie pomocou genetického algoritmu a simplexovej metódy. Zväčšite dimenziu problému na 3,4,5,6 dimenzíí a porovnajte výkonnosť GA zo simplexovou metódou.(kód napr. v http://www.techxhome.com/products/optsolve/ alebo http://www.ulib.org/webRoot/Books/Numerical_Recipes/bookcpdf.html
(podľa http://www.hao.ucar.edu/public/research/si/pikaia/tutorial.html)
(
tému vypracuje Michaela Ačová, 6acova@st.fmph.uniba.sk)Téma 4.
Evolúcia sortovacích sietí(max. fitness = 120)
GA vytvára 5-vstup
ové sortovacie siete obsahujúce najviac 9 porovnaní-výmen. Existuje 120 fitness prípadov (všetkých 5! permutácií sekvencie 1,2,3,4,5), a korektná sieť ich všetky zoradí bezchybne. Vyskúšaj koevolúciu pre zložitejšie prípady, kde sekvencie hodnôt sa vyvíjajú nezávisle a sú ohodnotené tým lepšie, čím viac sietí na nich zlyháva.(
tému vypracuje Peter Beňo, 8beno@st.fmph.uniba.sk)Téma 5.
Samoorganizácia kritických stavov v kopách piesku (sandpiles)Dvojdimenzionálna kopa piesku môže byť skonštruovaná na základe veľmi jednoduchých pravidiel pre jednoduchý celulárny automat. Stav bunky je charakterizovaný počtom zrniek piesku, ktoré obsahuje. Obnovovacie pravidlo hovorí, že keď má bunka 4 alebo viac zrniek piesku, stráca 4, a od každej z bezprostredne susediacich buniek so 4 alebo viac zrnkami dostáva jedno zrnko. Postupnosť stavov kopy môže teda vyzerať nasledovne
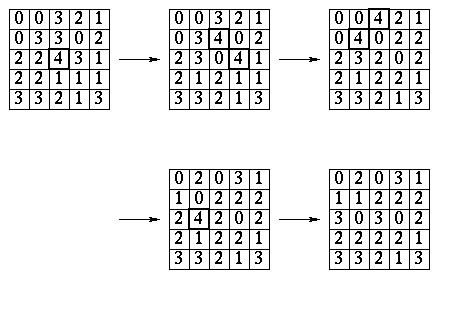
Celkovo 6 buniek bolo zahrnutých v lavíne, ktorá trvala 4 obnovovania.
Môžeme dostať túto mriežku do kritického stavu rýchlym pridávaním piesku do tabuľky dokiaľ rýchlosť prisypávania piesku nie je približne rovná rýchlosti, s ktorou zrnká piesku padajú z okrajov tabuľky. Ekvivalentný prístup je preťažiť tabuľku pieskom – dodať náhodné množstvo 5-8 zrniek do každého štvorca – a potom začať updatovať (bez pridávania ďalšieho piesku), dokiaľ tabuľka nedosiahne stabilný stav (obnova nespôsobí žiadne zmeny).
Zaujímavou charakteristikou tohto systému je, že keď je raz dosiahnuté kritického stravu, pridanie jedného zrnka piesku môže spôsobiť lavíny všetkých možných veľkostí, ktoré môžu trvať takmer ľubovolne dlho. Keď tento proces opakujeme veľa krát, vychádza nám, že N(S)
~ 1/Sa , N(S) je počet lavín veľkosti S (ovplyvňujúcich S buniek mriežky) a alfa je tzv. kritický exponent(Adaptované z
http://www.krl.caltech.edu/~charles/cns175/handouts/homework4.html)(
tému vypracuje Ján.Kováčik, Jan.Kovacik@st.fm.uniba.sk )
Téma 6
. Problém všeobecnej splniteľnosti (general satisfiability SAT), aj keď zahŕňame všetky druhy logických klauzúl, nie len konjunkcie a disjunkcie. Každý problém pozostáva z 20 boolovských premenných (A0 - A19) a a sady obmedzení. Cieľom je samozrejme nájsť pravdivostné priradenie ku každej premennej tak, že sú splnené všetky obmedzenia. V uvedených problémoch sú najlepšie riešenia pre človeka triviálne, ale GA nemá našu znalosť logiky a musí prehľadávať extenzívne. Pre každý z GA behov vykreslite graf sily(min,max a priemer).A)
5 konjunkcií, obmedzenia sú(A0 and A1 and A2 and A3)
(A4 and A5 and A6 and A7)
(A8 and A9 and A10 and A11)
(A12 and A13 and A14 and A15)
(A16 and A17 and A18 and A19)
c) Použite veľkosť populácie 50, 50 generácií, pmut = 0.01 a 3 rozdielne pravdepodobnosti kríženia: 0.1, 0.3 and 0.8. V čom sa líši správanie algoritmu pre dané 3 behy?
B) 10 konjunkcií, obmedzenia sú
(A0 and A1) (A2 and A3)
(A4 and A5) (A6 and A7)
(A8 and A9) (A10 and A11)
(A12 and A13) (A14 and A15)
(A16 and A17) (A18 and A19)
e) Zbehnite tento problém za rovnakých podmienok ako pri a, s rovnakou fitness funkciou. Aké sú rozdiely? Prečo sa objavili rozdiely, aj keď obmedzenia sú logicky ekvivalentné? Môžete pomocou použitej fitness funkcie vysvetliť rozdiel?
f) Zbehnite tento problém s populáciou veľkosti 100, 100 generáciách, pcross = 0.8, pri dvoch rozdielnych hodnotách pmut: 0.1 and 0.01. Aké sa objavili rozdiely? Môžete vysvetliť prečo sa objavili?
g) Vym
yslite novú fitness funkciu podstatne rozdielnu od prvej a testujte ju pre a) a e) s populáciou veľkosti 100, 100 generáciách, pcross = 0.8, pmut: 0.01. Aké sú výsledky v porovnaní s prvou fitness funkciou? Ako sa zmenil "povrch"?B) 7 disjunkcií, 4 konjunkcie, obmedzenia sú
(A0 or A1 or A2 or A3)
(not(A0) or not (A1))
(not(A0) or not(A2))
(not(A0) or not(A3))
(not(A1) or not(A2))
(not(A1) or not(A3))
(not(A2) or not(A3))
(A4 and A5 and A6 and A7)
(A8 and A9 and A10 and A11)
(A12 and A13 and A14 and A15)
(A16 and A17 and A18 and A19)
h) Testujte s populáciou veľkosti 100, 100 generáciách, pcross = 0.8, pmut: 0.1. s obidvoma Vámi navrhnutými fitness funkciami, vysvetlite rozdiely v správaní.
(Podľa
http://www.ifi.ntnu.no/~keithd/classes/mnfit378/homework/2000/assign1.html)(
tému vypracuje Pavol Šupa, supa@napri.sk)
Téma 7
. Použite simulované žíhanie pre riešenie pohybu koňa na šachovnici, kde zo zadaného poľa máte prebehnúť všetky ostatné poľa, pričom na každé pole vstúpite iba raz. Ako druhú časť úlohy riešte rovnaký problém s podmienkou, že sa kôň musí vrátiť naspäť. Pri riešení použite perturbáciu (mutáciu) toho druhu, že počiatok postupnosti polí do náhodne vybraného počtu polí skopírujete do nového riešenia a zvyšok vygenerujete. Úloha sa dá riešiť aj spätným prehľadávaním, ale len pre malé prípady.(
tému vypracuje Tomáš Pail, 8pail@st.fmph.uniba.sk)
Téma 8
. Zhodnoťte vplyv stratégií výberu na optimalizáciu pri použití definícií zhttp://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html
pre prepočítanie sily proporčne (viď formula 4.11c v knihe Evolučné algoritmy) alebo na základe usporiadania podľa veľkosti (formula 4.12b) a vlastný výber ruletou, turnajom, pomocou tzv. s
tochastic universal sampling, local selection, výber odrezaním najhorších (truncation selection) opísaných vhttp://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html
Zhodnoťte vplyv stratégií výberu na optimalizáciu nasledujúcich multimodálnych funkcií (pre n=1-10)
(zobraté z
http://www.aridolan.com/ga/gaa/gaa.html)Ackleyho funkcia
f(x) = 20+e-20*exp(-0.2*exp(sqrt((1/n)*sum(x(i)^2))-exp((1/n)*sum(cos(2*Pi*x(i)))
Rosenbrockova funkcia
f(x) = sum(100*(x(i)-x(i-1)^2)^2 + (1-x(i-1))^2
Schwefelova funkcia
f(x) = 418.9829*n + sum(-x(i)*sin(sqrt(abs(x(i))))
Rastriginova funkcia
f(x) = 10.0*n + sum(x(i)^2 - 10.0*cos(2*Pi*x(i)))
Griewankova funkcia
f(x) = 1/4000*sum(x(i)-100)^2 - prod((x(i)-100)/sqrt(i)) + 1
Sférický model
f(x) = sum((x(i)-1)^2)
Funkcie jednej premennej
f(x) = x^4 - 12*x^3 + 15*x^2 + 56*x - 60
minimalizácia funkcie viac premenných
f(x1,x2,x3,x4,x5) = x1*sin(x1) + 1.7*x2*sin(x1) - 1.5*x3 - 0.1*x4*cos(x4+x5-x1) + (0.2*x5^2-x2) - 1
Funkcia "blbeček" - maximalizácia pre 10 premenných
(x1*x2*x3*x4*x5)/(x6*x7*x8*x9*x10) kde (x1..x10)=[1..10]
(
tému vypracuje ...)Téma 9
. Zhodnoťte vplyv kríženia a mutácie pri optimalizácii pri použití definícií zhttp://www.systemtechnik.tu-ilmenau.de/~pohlheim/GA_Toolbox/algindex.html
pre kríženie
reálnych hodnôt: lineárnou kombináciou, priemerom, diskrétne a binárnych hodnôt: jednobodové, dvojbodové, viacbodové, uniformné a mutáciu binárnych premenných a reálnych premenných (z evolučných stratégií) pre funkcie daných v príklade 9.(
tému vypracuje ...)Téma 10
. Genetický algoritmus pre úlohu Number Partitioning Problem. Použite oba prístupy na kódovanie zobrazenia p , tak priamo pomocou N-tice celých čísel, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.(
tému vypracuje Ján Hnila, hnila@dcs.fmph.uniba.sk)
Máte za úlohu použiť genetický algoritmus na riešenie problému priradenia úloh. Súbor úkolov musí byť urobený na množine procesorov. Každý úkol je definovaný dvoma časmi: časom potrebným na výpočet úkolu a časom potrebným na prenos výsledkov na hlavný procesor, p0. Všetky procesory zdieľajú jeden alebo viac komunikačných kanálov a každým kanálom sa d
á posielať iba jeden výsledok v danom čase, nie je možné paralelné zdieľanie kanálu. Úkoly ktoré prebiehajú na hlavnom procesore spotrebujú nulový komunikačný čas. Keď nie sú žiadne komunikačné kanály volné, procesor musí čakať aby vykonal komunikačnú časť svojho momentálneho úkolu. Cieľom je určiť rozvrh, teda sadu priradení úloh procesorom, ktorý by minimalizoval čas, kedy budú splnené všetky úkoly.Použitie GA na vyriešenie problému vyžaduje 2 základné prvky:
1. indivídua reprezentujúce rozvrhy a populácie rozvrhov
2 simulátor ktorý spočíta celkový čas, kedy je rozvrh ukončený
Pre inšpiráciu pozri napr.
http://www-ra.informatik.uni-tuebingen.de/mitarb/schwehm/MYpapers/JAR98.ps.gzPouži svoj program na vyriešenie úkolov s dvojicami výpočtového a komunikačného času:
(7 16) (11 22) (12 40) (15 22) (17 23)
(17 23) (19 23) (20 28) (20 27) (26 27)
(28 31) (36 37) (31 29) (28 22) (23 19)
(22 18) (22 17) (29 16) (27 16) (35 15)
Podľa Kidwella (1993) je minimálny čas na ukončenie úkolov na 3 procesoroch s jedným komunikačným kanálom 202 časových krokov. Pokúste sa nájsť toto riešenie Vaším genetickým algoritmom, pričom je dôležitý výber Vašej fitness funkcie. Opíšte úspešnosť pomocou grafov v závislosti na hodnotách kľúčových parametrov ako je rýchlosť mutácií a percento kríženia, počet bodov kríženia, veľkosť populácie a selekčný mechanizmus. (Podľa http://www.idi.ntnu.no/~keithd/classes/evcomp/homework/assign2.html)
(
tému vypracuje Alexander Moravcik, 7moravcik@st.fmph.uniba.sk)Téma 12.
Mravčie algoritmyPoužite článok o graph partitioning http://www-iasc.enst-bretagne.fr/PROJECTS/SWARM/Papers/ecal.ps.gz
a stránku
http://www-iasc.enst-bretagne.fr/PROJECTS/SWARM/graph.htmlako základ pre Váš algoritmus, kde pre pravdepodobnosti zobratia a upustenia vrcholu ![]() a
a ![]()
použite iné mocniny ako je druhá mocnina a na grafu zobrazte výsledky efektivity optimalizácie v závislosti na tejto mocnine.
(Pozri
http://iridia.ulb.ac.be/~mdorigo/ACO/tutorials-courses.html)(
tému vypracuje Matúš Kalaš, 8kalas@nw.fmph.uniba.sk)
Téma 13.
PerkolácieKeď sa vám zrazí mlieko alebo sa porežete a začnete krvácať, ide vlastne o podobné procesy. Tzv. sol-gel transition (prechod), konverzia kvapaliny na polotuhú látku, ktorá vzniká ako výsledok náhodného spájania molekúl. Tento proces, ktorý je analogický tomu, keď si ľudia v davu náhodne pospájajú ruky, je charakteristickou črtou percolation phenomenon (perkolácie).
Perkolácia je spojená s menom P.G. de Gennesa, nosit
Random Site Percolation
(RSP)Príklad clusteru veľkosti 5 je:
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
Za predpokladu, že
p je pravdepodobnosť pre každú bunku byť obsadenou (teda ohodnotenou 1)aký je očakávaný počet klastrov veľkosti 3 na mriežke? (Pre jednoduchosť ignorujte okrajové efekty).Vo väčšine prípadov je nemožné určiť kritickú pravdepodobnosť objavenia sa nekonečného klusteru (teda takého, ktorý siaha z jednej strany mriežky na druhú). Pre
64x64 rpravideľnú štvorcovú mriežku experimentálne určite kritickú pravdepodobnosť testovaním, či sa objavil "nekonečný kluster" pre p (pravdepodobnosť medzi 0 a 1). To zistíte generovaním náhodných konfigurácií pre fixné p toľkokrát, aby ste dostali podiel prípadov, kedy sa objavil nekonečný kluster, a tento postup opakujte pre rozdielne p. Zobrazte pravdepodobnosť nájdenia nekonečného klusteru proti pravdepodobnosti p.(Podľa http:
//www.krl.caltech.edu/~charles/cns175/handouts/homework4.html)(
tému vypracuje ...)Téma 14.
Genetické programovanie pre mravca hľadajúceho cestuGenetickým programovaním vytvoriť "program" pre mravca pomocou súboru pravidiel. Mravec má zberať potravu rozsiatu na nie celkom súvislej dráhe umiestnenej na toroidálnej mriežke, pričom má iba obmedzené senzory (teda vidí iba na vedľajšie bunky mriežky). Mravec má za daný počet časových krokov zozberať čo najviac potravy. V detailoch zadania sa možno inšpirovať na http://www2.informatik.uni-erlangen.de/~jacob/Evolvica/GP/Java/html/ant/ant.html). Úlohou je vygenerovať pravidlá a) pre vlastnú náhodne vygenerovanú dráhu s podobnými vlastnosťami ako je John Muir Trail z vyše uvedenej WWW stránky. b) Vyskúšať vygenerovanie pravidiel, ktoré by platili pre viac dráh súčasne.
(
tému vypracuje Aleksandra Takáč, Aleksandra.Takac@st.fmph.uniba.sk)
Vypracované "case studies" v šk.r. 2001/2002
Vypracované "case studies" v šk.r. 2000/2001
viď
http://math.chtf.stuba.sk/evol/prednaska00.htm naspodku strany
Vypracované "case studies" v šk.r. 1999/2000
viď
http://math.chtf.stuba.sk/evol/prednaska99.htm naspodku strany