2.4.3 Algoritmus učenia perceptróna
Najprv uká¾eme algoritmus procesu uèenia - teda
hľadania vhodných synaptických váh, a potom pre
tento algoritmus doká¾eme vetu o konvergencii perceptrónu, tj.
doká¾eme, ¾e po koneènom poète krokov JPR sa dostane
do stavu, v ktorom obidve triedy vie separovať.
Postup uèenia JPR bude teda nasledovný:
Prepokladajme, že
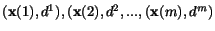 je trénujúca vzorka vektorov, na ktorej sa bude
perceptrón uèiť,
je trénujúca vzorka vektorov, na ktorej sa bude
perceptrón uèiť,
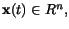
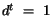 ,
ak
,
ak
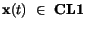 ,
,
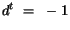 ,
ak
,
ak
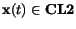 .
.
![]() je trénujúca vzorka vektorov, na ktorej sa bude
perceptrón uèiť,
je trénujúca vzorka vektorov, na ktorej sa bude
perceptrón uèiť,
![]()
![]() ,
ak
,
ak
![]() ,
,
![]() ,
ak
,
ak
![]() .
.