|
|
|
|
| (4.48) |
| (4.49) |
| (4.50) |
| (4.51) |
| (4.52) |
| (4.53) |
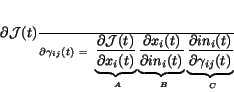 |
(4.54) |
| (4.55) |
| (4.56) |
| (4.57) |
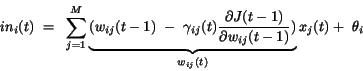 |
(4.58) |
| (4.59) |
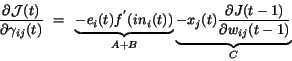 |
(4.60) |
| (4.61) |
| (4.62) |
| (4.63) |
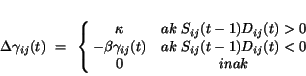 |
(4.64) |
| (4.65) |
| (4.66) |
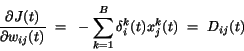 |
(4.67) |
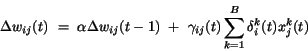 |
(4.68) |
| (4.69) |
| QCE | ||||
| CE | malé | stredné | veľké | veľmi veľké |
| veľmi malé | malé | malé | stredné | veľké |
| malé | malé | stredné | stredné | veľké |
| stredné | malé | stredné | stredné | veľké |
| veľké | malé | stredné | veľké | veľké |
| veľmi veľké | malé | stredné | veľké | veľké |
|