2.1.1 Problém obchodného cestujúceho (TSP)
Majme danú mno¾inu 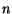 miest a vzdialenos»
miest a vzdialenos» 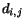 pre v¹etky dvojice miest
pre v¹etky dvojice miest 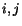 .
Potrebujeme zisti», v akom
poradí má obchodný cestujúci prechádza» mestá tak, aby sa
vrátil do mesta, z ktorého vyrazil a zároveò ka¾dé mesto na
trase nav¹tívil práve jedenkrát. Podmienkou v¹ak je, ¾e
vzdialenos», ktorú precestoval, je najkrat¹ia mo¾ná. Rie¹enie tohto problému je prípustné, ak sú splnené
nasledujúce obmedzenia :
.
Potrebujeme zisti», v akom
poradí má obchodný cestujúci prechádza» mestá tak, aby sa
vrátil do mesta, z ktorého vyrazil a zároveò ka¾dé mesto na
trase nav¹tívil práve jedenkrát. Podmienkou v¹ak je, ¾e
vzdialenos», ktorú precestoval, je najkrat¹ia mo¾ná. Rie¹enie tohto problému je prípustné, ak sú splnené
nasledujúce obmedzenia :
- obchodný cestujúci prechádza ka¾dým mestom práve
jedenkrát,
- jeho cesta v grafe tvorí cyklus.
Prípustnos» rie¹enia je teda daná nájdením
hamiltonovskej kru¾nice a mieru optimality rie¹enia
popisuje súèet vzdialeností medzi mestami na hamiltonovskej
kru¾nici.
Neurónová sie», ktorá tento problém rie¹i, musí
vyjadri» pre dané mesto, ktoré mesto mu predchádza a ktoré
mesto za ním nasleduje. Toto je vyjadriteµné v sieti s 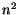 neurónmi pri maticovom usporiadaní uvedenom na obr. 2.2
neurónmi pri maticovom usporiadaní uvedenom na obr. 2.2
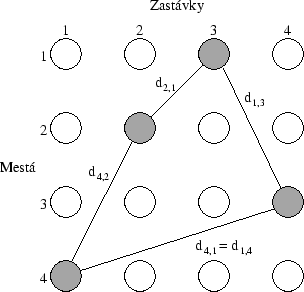
Obrázok 2.2:
Návrh neurónovej siete pre TSP pri  .
Kvôli
prehµadnosti nie sú zakreslené prepojenia neurónov.
Rie¹enie je zobrazené pomocou èiar. Rie¹ením je
postupnos» miest 4-2-1-3, prípadne jej cyklická
premutácia.
.
Kvôli
prehµadnosti nie sú zakreslené prepojenia neurónov.
Rie¹enie je zobrazené pomocou èiar. Rie¹ením je
postupnos» miest 4-2-1-3, prípadne jej cyklická
premutácia.
 |
Je zrejmé, ¾e usporiadanie v tomto tvare pomáha pri pochopení
rie¹enia, inak je nepodstatné. Vz»ah pre energiu siete
je mo¾né upravi» pomocou zavedenia dvoch indexov pre
jeden neurón. Jedná sa len o technickú úpravu vz»ahu,
význam zostane nezmenený.
Teraz sformulujeme túto úlohu pomocou novej
sústavy dvojstavových premenných tak, aby hµadanie
prípustného rie¹enia mohlo by» vyjadrené ako
minimalizácia funkcie týchto nových premenných.
Zadefinujme maticu 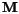 typu
typu 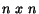 s prvkami
s prvkami 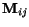 ,
ktoré
nadobúdajú hodnoty
,
ktoré
nadobúdajú hodnoty 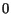 alebo
alebo 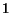 ,
pre
,
pre 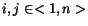 .
.
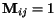 vtedy, keď obchodný cestujúci prechádza
mestom
vtedy, keď obchodný cestujúci prechádza
mestom 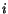 v
v 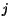 -tom kroku. V opaènom prípade
-tom kroku. V opaènom prípade
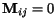 .
V podstate hodnoty
.
V podstate hodnoty 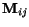 sú ekvivalentom hodnotám
neurónov
sú ekvivalentom hodnotám
neurónov 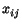 .
Prípustnému rie¹eniu pôvodnej úlohy teraz zodpovedá stav
matice, ktorý sa dá popísa» nasledovne :
.
Prípustnému rie¹eniu pôvodnej úlohy teraz zodpovedá stav
matice, ktorý sa dá popísa» nasledovne :
- v ka¾dom riadku je najviac jedna jednièka, tj. pre
x-te mesto platí
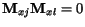 ,
ak
,
ak 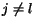 ,
,
- v ka¾dom ståpci je najviac jedna jednièka, tj. pre
x-ty krok obchodného cestujúceho platí
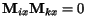 ,
ak
,
ak 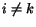 ,
,
- v matici je práve
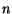 jednièiek, tj.
jednièiek, tj.
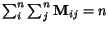 ,
,
- súèet vzdialeností medzi mestami je urèený maticou
vzdialeností, prièom celková då¾ka cesty je
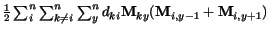
Teraz vytvoríme funkcie 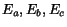 a
a 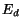 ,
ktoré nadobúdajú minimálne hodnoty pri splnení predchádzajúcich
podmienok. Funkcie sú vytvárané na základe vz»ahov
uvedených v týchto podmienkách.
,
ktoré nadobúdajú minimálne hodnoty pri splnení predchádzajúcich
podmienok. Funkcie sú vytvárané na základe vz»ahov
uvedených v týchto podmienkách.
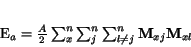 |
(2.7) |
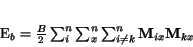 |
(2.8) |
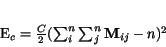 |
(2.9) |
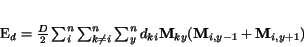 |
(2.10) |
Vo vz»ahoch (2.7) - (2.10) A, B, C a D sú voliteµné parametre.
Tak¾e rie¹enie je optimálne, ak
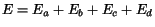 nadobúda svoje minimum. Na tomto mieste je vhodné pripomenú» si,
ako vyzerá energetická funkcia pre diskrétny model Hopfieldovej siete pri
maticovom oèíslovaní neurónov:
nadobúda svoje minimum. Na tomto mieste je vhodné pripomenú» si,
ako vyzerá energetická funkcia pre diskrétny model Hopfieldovej siete pri
maticovom oèíslovaní neurónov:
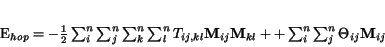 |
(2.11) |
Prepísaním (2.7),(2.8),(2.9) a (2.10) na tvar energetickej funkcie (2.11)
dosiahneme to, ¾e tvar "na¹ej" funkcie 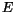 bude
ekvivalentný tvaru funkcie
bude
ekvivalentný tvaru funkcie 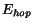 ,
ktorá sa poèas konvergencie
siete minimalizuje (základná vlastnos» Hopfieldovej siete).
Po tomto prepísaní nám teda bude staèi»
porovna» výsledky s (2.11) a µahko vypoèítame nastavenie
váh a prahov. Nasledujúce úpravy spoèívajú v zavedení
symbolu Croneckerovo delta, tj.
,
ktorá sa poèas konvergencie
siete minimalizuje (základná vlastnos» Hopfieldovej siete).
Po tomto prepísaní nám teda bude staèi»
porovna» výsledky s (2.11) a µahko vypoèítame nastavenie
váh a prahov. Nasledujúce úpravy spoèívajú v zavedení
symbolu Croneckerovo delta, tj. 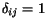 ,
ak
,
ak 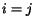 ,
inak
,
inak 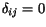 ,
èo nám umo¾ní doplni» do
niektorých výrazov ďal¹ie sumy.
Z (2.7) vyplýva
,
èo nám umo¾ní doplni» do
niektorých výrazov ďal¹ie sumy.
Z (2.7) vyplýva
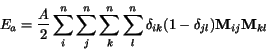 |
(2.12) |
Výraz
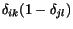 je rovný
je rovný 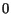 ,
ak
,
ak 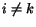 alebo
alebo 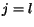 .
.
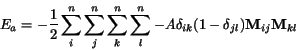 |
(2.13) |
Tento výraz je vlastne výraz (2.11), kde
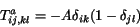 |
(2.14) |
Analogicky z (2.8) dostaneme
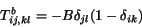 |
(2.15) |
Z (2.9) dostaneme
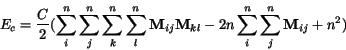 |
(2.16) |
Po prenásobení výrazu v zátvorke výrazom 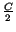 dostaneme
dostaneme
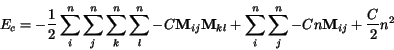 |
(2.17) |
Preto¾e posledný èlen
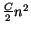 nezmení polohu minima
vy¹¹ie uvedenej funkcie
nezmení polohu minima
vy¹¹ie uvedenej funkcie 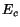 ,
zanedbáme ho a dostávame
,
zanedbáme ho a dostávame
 |
(2.18) |
Zo (2.10) vyplýva
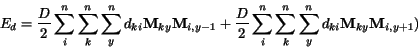 |
(2.19) |
prièom platí, ¾e 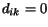 ,
ak
,
ak 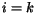 .
Zavedením
Croneckerovho symbolu
.
Zavedením
Croneckerovho symbolu 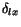 a nahradením indexu
a nahradením indexu 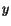 indexom
indexom 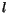 vo výraze pre
vo výraze pre 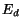 dostávame
dostávame
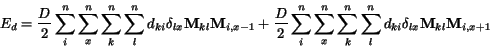 |
(2.20) |
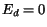 ,
ak
,
ak 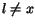 .
Polo¾íme
.
Polo¾íme 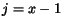 v prvej èasti výrazu a
v prvej èasti výrazu a 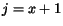 v druhej
èasti a dostaneme
v druhej
èasti a dostaneme
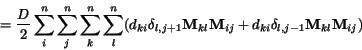 |
(2.21) |
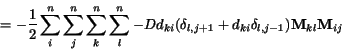 |
(2.22) |
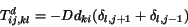 |
(2.23) |
Tak¾e nakoniec pre nastavenie váh prepojení v sieti
medzi neurónmi 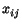 a
a 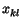 bude plati»
bude plati»
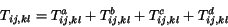 |
(2.24) |
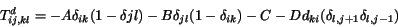 |
(2.25) |
Po odvodení vy¹¹ie uvedených vz»ahov mo¾eme
uvies» nasledujúci algoritmus:
ALGORITMUS pre TSP:
Krok 1. Priradenie váh prepojeniam
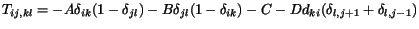 pre
pre
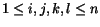 ,
- A,B,C,D sú zvolené parametre siete (sú meniteµné),
,
- A,B,C,D sú zvolené parametre siete (sú meniteµné),
Krok 2. Inicializácia
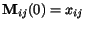 ,
pre
,
pre
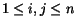 ,
V tejto formule
,
V tejto formule
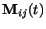 je výstup vrcholu ,,ij'' v èase
je výstup vrcholu ,,ij'' v èase 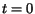 a
a 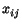 je náhodná premenná, ktorá nadobúda hodnotu 0 alebo 1.
je náhodná premenná, ktorá nadobúda hodnotu 0 alebo 1.
Krok 3. Iterácia pokiaµ sie» neskovergovala
![$ {\bf M}_{ij}(t+1) = g_h [\sum_{k=1}^n \sum_{i=1}^n T_{ij,kl}. {\bf M}_{kl}(t) ]$](img98.gif) pre
pre
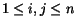 .
Krok konèí, ak sie» skonvergovala, tj. jej stav sa
u¾ nemení. Tu mô¾e dôjs» k zacykleniu siete.
.
Krok konèí, ak sie» skonvergovala, tj. jej stav sa
u¾ nemení. Tu mô¾e dôjs» k zacykleniu siete.
Krok 4. Opakovanie od kroku 2.
Ak do¹lo k zacykleniu siete, je potrebný nový výpoèet
zaèínajúci nastavením nových poèiatoèných
hodnôt siete. Tie¾ je mo¾né zmeni» parametre siete
a nastavi» nové váhy, tj. zaèa» krokom 1.

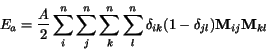
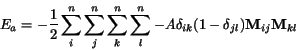
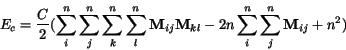
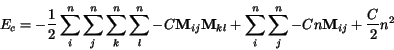
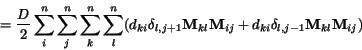
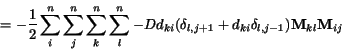
![]() pre
pre
![]() ,
- A,B,C,D sú zvolené parametre siete (sú meniteµné),
,
- A,B,C,D sú zvolené parametre siete (sú meniteµné),
![]() ,
pre
,
pre
![]() ,
V tejto formule
,
V tejto formule
![]() je výstup vrcholu ,,ij'' v èase
je výstup vrcholu ,,ij'' v èase ![]() a
a ![]() je náhodná premenná, ktorá nadobúda hodnotu 0 alebo 1.
je náhodná premenná, ktorá nadobúda hodnotu 0 alebo 1.
![]() pre
pre
![]() .
Krok konèí, ak sie» skonvergovala, tj. jej stav sa
u¾ nemení. Tu mô¾e dôjs» k zacykleniu siete.
.
Krok konèí, ak sie» skonvergovala, tj. jej stav sa
u¾ nemení. Tu mô¾e dôjs» k zacykleniu siete.