Prednáška "Evolučné algoritmy"

MFF UK, 4. ročník, odbor "informatika"

Šk.r. 2001/02, semester zimný

Dátum prednášky: utorok o 11.30 hod, poslucháreň V

---

---

Sylabus prednášky:

Prednášajúci: Prof. V. Kvasnička {kvasnic@cvt.stuba.sk}a Doc. J. Pospíchal {pospich@cvt.stuba.sk}

Katedra matematiky CHTF STU,

Semester: zimný

Rozsah: 2-0-0

1. Základné pojmy evolučných algoritmov – optimalizačný problém a jeho kódovanie, binárna reprezentácia reálnej premennej, transformácia spojitého optimalizačného problému na binárny optimalizačný problém.

2. Horolezecké (hill climbing) algoritmy – elementárne stochastické optimalizačné algoritmy, slepý algoritmus a horolezecký algoritmus, horolezecký algoritmus s učením, metóda zakázaného hľadania (tabu search), evolučné programovanie.

3. Genetický algoritmus – darvinovská evolúcia v živej prírode, základné pojmy, populácia a sila (fitness) chromozómov, kríženie chromozómov, implementácia genetického algoritmu, teória genetického algoritmu, Hammingova bariéra, ”messy” chromozómy, paralelná implementácia genetického algoritmu.

4. Genetické programovanie – základné pojmy z teórie grafov, koreňové stromy a Readov kód, symbolická regresia, rekonštrukcia stromov s požadovanými vlastnosťami, kódovanie funkcií pomocou acyklických orientovaných grafov.

5. Simulované žíhanie – základné pojmy, vzťah k štatistickej fyzike, paralelná implementácia.

6. Kombinatoriálne optimalizačné problémy – klasifikácia, základné úlohy z teórie grafov a operačného výskumu, špecifikácie operátorov mutácie a kríženia pre kombinatoriálne optimalizačné problémy.

7. Evolučné stratégie – historické poznámky, stratégia (1+1) - jeden rodič a jeden potomok, distribúcia pravdepodobnosti, generovanie náhodných čísel, viacčlenné stratégie a kovariancie, súvislosti s evolučným programovaním.

8. Neurónové siete – klasifikácia neurónových sietí, neurónové siete s dopredným šírením, rekurentné neurónové siete, parametrická adaptácia neurónových sietí pomocou gradientovej optimalizačnej metódy, adaptácia neurónových sietí ako stochastický optimalizačný problém, štrukturálna adaptácia neurónových sietí pomocou evolučných algoritmov.

9. Umelý život – definície života a umelého života, umelá inteligencia a multiagentové systémy, kognitívne aparáty agentov, darvinovská evolúcia multiagentových systémov, emergencia kooperatívnych vlastnosti. Celulárne automaty, evolúcia pravidiel, vznik komplexných javov. Kooperácia, súťaženie, altruizmus, dilema väzňov a tragédia spoločného. Emergencia zložitosti, vznik života evolúciou neživého.

10. DNA výpočty – základné pojmy z molekulovej biológie, štruktúra a vlastnosti DNA, teoretické modely výpočtového procesu, experiment L. Adlemana s hľadaním hamiltónovskej cesty v orientovanom grafe pomocou DNA, DNA počítače in vivo.

Literatúra:

1. V. Kvasnička, J.Pospíchal a P. Tiňo: Evolučné algoritmy, STU Bratislava 2000..

2. T. Bäck: Evolutionary Algorithms in Theory and Practice - Evolutionary Strategies, Evolutionary Programming, Genetic Algorithms. Oxford University Press, Oxford, UK, 1996.

3. Z. Michaliewicz: Genetic Algorithms + Data Structures = Evolution Programs. Springer Verlag, Berlin, 1992.

4. W. Banzhaf, P. Nordin, R. E. Keller, and F. D. Francone: Genetic Programming – An Introduction. Morgan Kaufmann Publishers, San Francisco, 1998.

Charles Darwin "On the Origin of Species" (doc)

Úvodná kapitola z knihy "Evolutionary Design by Computers", editor Peter J. Bentley

ISBN 1-55860-605-X, domovská stránka knihy je na adrese

http://www.mkp.com/books_catalog/1-55860-605-x.asp

text kapitoly pdf.

Tutoriál od Prof. Hans-Paul Schwefel "On Natural Life's Tricks to Survive and Evolve"

(pdf alebo ps.zip)

Tutorial od Prof. John Koza (University of Stanford) "Genetic Programming: Biologically Inspired Computation that Creatively Solves Non-Trivial Problems" (pdf)

 Tutorial od Prof. Darrell Whitley "A Genetic Algorithm Tutorial" (pdf)

Predbežné texty ku knihe "Evolučné algoritmy"

Jednotlivé kapitoly môžu slúžiť ako základný text prednášky, kde sú uvedené aj príklady na precvičenie.

Obsah

Kapitola 1- Úvodné poznámky (ps.zip alebo pdf)

Kapitola 2 - Základné pojmy evolučných algoritmov (ps.zip alebo pdf)

Kapitola 3 - Horolezecké algoritmy (ps.zip alebo pdf)

Kapitola 4 - Genetické algoritmy (ps.zip alebo pdf)

Kapitola 5 - Genetické programovanie (ps.zip alebo pdf)

Kapitola 6 - Simulované žíhanie (ps.zip alebo pdf)

Kapitola 7 - Kombinatoriálne optimalizačné problémy (ps.zip alebo pdf)

Kapitola 8 - Evolučné stratégie (ps.zip alebo pdf)

Kapitola 9 - Umelý život (ps.zip alebo pdf)

Kapitola 10 - Neurónové siete (ps.zip alebo pdf)

1. prednáška

Všeobecné predstavy o darvinovskej evolúcii, chápanie evolúcie ako algoritmu, význam učenia v evolúcii (Baldwinov efekt), mémy (Dawkins) ako nosič informácie pre chromozómy.

Priesvitky k prednáške (ps.zip alebo pdf)

Pozri tiež pripravovaný článok "Umelá evolúcia" (ps.zip alebo pdf)

2. prednáška

Binárne kódovanie reálnej premenne, transformácia spojitého optimalizačného problému na binárny optimalizačný problém. Slepý algoritmus, horolezecký algoritmus (hill climbing), horolezecký algoritmus a učením, metóda zakázaného prehľadávania (tabo search), evolučné programovanie. Predmet tejto prednášky odpovedá 2. a 3. kapitole knihy "Evolučné algoritmy".

Priesvitky k prednáške (ps.zip alebo pdf)

3. prednáška

Genetické algoritmy, "messy" genetický algoritmus, paralélny genetický algoritmus. Základné princípy genetických algoritmov.

Priesvitky k prednáške (ps.zip alebo pdf)

4. prednáška

Teória genetických algoritmov.

Priesvitky k prednáške (ps.zip alebo pdf)

5. prednáška

Genetické programovanie, symbolická regresia.

Priesvitky k prednáške (ps.zip alebo pdf)

6. prednáška

Simulované žíhanie.

Priesvitky k prednáške (ps.zip alebo pdf)

7. prednáška

Kombinatoriálne optimalizačné problémy. Úloha obchodného cestujúceho, Number Partitioning Problem.

Priesvitky k prednáške (ps.zip alebo pdf)

8. prednáška

Evolučné stratégie.

Priesvitky k prednáške (ps.zip alebo pdf)

9. prednáška

Umelý život.

Priesvitky k prednáške (ps.zip alebo pdf)

10. prednáška

Neurónové siete.

Priesvitky k prednáške (ps.zip alebo pdf)

11. prednáška

Swarm výpočty.

Priesvitky k prednáške (ps.zip alebo pdf)

12. prednáška

Podrobnosti o skúške, témy "case studies" (ps.zip alebo pdf)

Témy "case studies" z predmetu "Evolučné algoritmy"

Skúška z prednášky "Evolučné algoritmy" bude udelená na základe vypracovanej "case study" z oblastí uvedených nižšie. "Case study" je písomná práca v rozsahu približne 7-10 strán (page size A4, font size 10, line spacing single), obsahuje teoretický popis použitej metódy a získané numerické výsledky, ktoré sú ilustrované tabuľkami a grafmi. Integrálnou prílohou "case study" bude aj fungujúci program, pomocou ktorého bola vypracovaná jej aplikačná časť.

Skúška sa uskutoční na Katedre matematiky FCHPT STU vždy v piatok v intervale od 9-11 hod., na skúšku je potrebné sa prihlásiť na t.č. 59325104/59325294, alebo emailom {kvasnic,pospich}@cvt.stuba.sk

Každá téma z "case study" bude mocť byť použitá iba jedným študentom, na tému sa treba prihlásiť a postupné "prideľovanie" bude prebiehať podľa pravidla “kto skôr príde..”. Podstatou skúšky bude diskusia o riešenej úlohe a taktiež všeobecné vedomosti z evolučných algoritmov.

Upozornenie: Záujemci o skúšku pošlú e-mailom aspoň jeden deň pred konaním skúšky ako attachment (do 16.00 hod.) vypracovanú "case study" na adresy {kvasnic,pospich}@cvt.stuba.sk , a musia sa uistiť, že sme ich súbor dostali v poriadku (pozor, musí byť do 2 MB), alebo sa dohodnú na inom spôsobe dodania súboru. Súbor má byť v PS alebo v PDF formáte, pričom "čitateľnosť" súborov nech je prekontrolovaná pomocou GhostView-u alebo AcrobatReader-u. Práce budú vystavené na tejto stránke pre poučenie budúcich generácií.

Ako vytvoriť PS dokument pomocou MS WORD-u: Priradí sa poscriptovská tlačiareň a nechá sa tlačiť do súboru (print to file), takto vznikne PS súbor, je potrebné ho ešte prekontrolovať pomocou GhostView, či sa vytvoril korektne.

Téma 1. Horolezecký algoritmus pre funkciu f(x) definovanú v

pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokúste sa optimalizovať parametre c₀ a P_mut tak, aby ste skoro so 100% istotou dostali globálne minimum s čo najmenším počtom iteračných krokov.

(tému vypracuje Patrik Sucansky, p3k@goatrance.com)

Téma 2. Metóda zakázaného hľadania aplikovanú na TSP (riešenie obchodného cestujúceho), pričom cesta nech je vyjadrená pomocou permutácie. Transformačné operátory tÎ S sú realizované ako permutácie transpozícií dvoch objektov. Operátor t_ij pôsobí na permutáciu P ako transpozícia objektov i a j,

pre i<j. Ako testovací príklad použite ortogonálnu mriežku bodov - miest, kde sa vzdialenosť počíta pomocou Hammingovej metriky (pozri príklad 8.2). Pokúste sa o optimalizáciu veľkosti "s" zakázaného zoznamu T (tabu listu) a maximálneho počtu iterácií time_max pre rôzne hodnoty N dimenzie ortogonálnej mriežky bodov, N=4,5,...,10, tak , aby ste s 95% pravdepodobnosťou dostali korektný výsledok. Podobné úvahy vykonajte aj pre suboptimálne výsledky, ktoré sa líšia len niekoľko málo jednotiek od optimálneho výsledku.

(tému vypracuje Ľudovít Hamaj, 9hamaj@st.fmph.uniba.sk)

Téma 3. Metóda zakázaného hľadania aplikovaná na úlohu N dám na šachovnici. Hľadá sa také umiestnite N dám na šachovnici N´ N tak, aby v každom riadku, stĺpci a diagonále bola umiestnená práve jedna dáma (t.j. neexistuje kolízne postavenie medzi dámami). Zložitosť riešenia tohto problému silne závisí od zvolenej reprezentácie postavenia dám na šachovnici. Jednoduchá reprezentácia postavenia dám je pomocou permutácie P=(p₁, p₂, ..., p_N). Potom dámy na šachovnici sú umiestnené takto: v 1. stĺpci na p₁-tom riadku, v 2. stĺpci na p₂-tom riadku, atď. Táto jednoduchá reprezentácia rozmiestnenia dám na šachovnici pomocou permutácií má výhodu v tom, že v každom stĺpci a riadku šachovnice sa nachádza práve jedna dáma. Každej permutácii N objektov priradíme celé nezáporné číslo col(P), ktoré odpovedá počtu diagonálnych kolízií. Riešenie problému je potom taká permutácia P, ktorá má nulový počet kolízií, col(P)=0. Funkcia col(P) je určená vzťahom

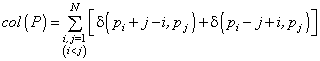
kde d (i,j) je Kroneckerovo delta, d (i,j)=1, pre i=j, d (i,j)=0, pre i¹ j.

(tému vypracuje XXX, XXX@st.fmph.uniba.sk)

Téma 4. Genetický algoritmus pre funkciu

pre xÎ [-10,10]. Premenná x je binárne reprezentovaná tak v štandardnom kódovaní, ako aj v Grayovom kódovaní. Pokuste sa nájsť minimálnu veľkosť populácie a také hodnoty pravdepodobností P_cross a P_mut, aby ste skoro so 100% istotou dostali globálne minimum s predpísaným minimálnym počtom krokov.

(tému vypracuje Marek Dorsic, marek.dorsic@st.fmph.uniba.sk)

Téma 5. Genetický algoritmus pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke. Použite oba prístupy na kódovanie cesty, tak priamo pomocou permutácie, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.

(tému vypracuje Jan Michalička, jan.michalicka@st.fmph.uniba.sk)

Téma 6. Genetický algoritmus pre úlohu Number Partitioning Problem. Použite oba prístupy na kódovanie zobrazenia p , tak priamo pomocou N-tice celých čísel, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.

(tému vypracuje Miloš Hasan, milos.hasan@inmail.sk)

Téma 7. Algoritmus simulovaného žíhania pre úlohu obchodného cestujúceho na ortogonálnej štvorcovej mriežke. Použite oba prístupy na kódovanie cesty, tak priamo pomocou permutácie, ako aj pomocou binárneho reťazca (pozri cvičenie 7.1 z kapitoly Kombinatoriálne optimalizačné problémy). Porovnajte efektívnosť týchto dvoch rôznych prístupov.

(tému vypracuje Juraj Ursíny, 8URSINY@turing.fmph.uniba.sk)

Téma 8. Evolučná stratégia (1+1). Metódu aplikujete na hľadanie globálneho minima funkcie

pre xÎ [-10,10], ktorá je zovšeobecnená pre viacrozmerný prípad takto

Použite pravidlo zmeny s 1/5 úspešnosti a nakreslite graf, kde na vodorovnej osi bude počet generácií a na zvislej aktuálna funkčná hodnota rodiča.

(tému vypracuje XXX, XXX@st.fmph.uniba.sk)

Téma 9. Genetické programovanie: Implementuje genetický algoritmus (pozri algoritmus 3.5) tak, že chromozómy budú určené ako Readove lineárne kódy s ohodnotením vrcholov podľa (5.18-19). Toto ohodnotenie nech je vykonané tak, že syntaktické stromy budú odpovedať Boolovským funkciám (t.j. funkčné vrcholy sú operácia and, or, xor, a not, a terminálové vrcholy sú jednotlivé Boolovské premenné). Účelová funkcia (5.24) nech je rozšírená o pokutový člen, ktorý bude preferovať syntaktické stromy s menším počtom vrcholov

kde a je malá kladná konštanta a symbol |t| vyjadruje počet vrcholov v strome t. Modifikujete napísanú implementáciu tak že bude odpovedať horolezeckému algoritmu. Porovnajte efektívnosť týchto troch rozdielnych metód pri konštrukcii funkcií, ktoré reprodukujú predpísanú regresnú tabuľku.

(tému vypracuje Martin Homola, homola@adela.sk)

Téma 10. Použitie genetického algoritmu na adaptáciu neurónovej siete. Implementujte neurónovú sieť s dopredným šírením signálu, ktorá obsahuje jednu vrstvu skrytých neurónov a so sigmoidálnou prechodovou funkciou. Použitím genetického algoritmu adaptujte túto neurónovú sieť (t.j. váhy a prahové koeficienty) siete tak, aby s čo najmenšou chybou produkovala rôzne Boolovské funkcie, pričom z numerických dôvodov namiesto hodnoty Boolovských premenných 0 a 1 budeme brať 0.1 a 0.9.

(tému vypracuje Matúš Navarčík, Matus.Navarcik@st.fmph.uniba.sk)

Téma 11. L-systém (tvorba "kríka") je daný nasledovnými pravidlami: (1) štartovný bod F, (2) produkčné pravidlo F ® F [+F][-F], kde F znamená "nakresli čiaru" (začíname kolmou čiarou z počiatočného bodu so súradnicami 0,0 do koncového bodu so súradnicami 0,10). Symbol [ znamená zapamätať si súradnice koncového bodu a zodpovedajúcu zmenu súradníc

dx= x koncový - x počiatočný , dy= y koncový - y počiatočný

Symbol ] znamená vrátiť sa na zapamätané súradnice bodu a zodpovedajúce dx a dy, symbol + znamená otočiť sa doľava (použili sme prepis pre súradnice nového bodu

x koncový = x počiatočný + 0.7 (cos(40^o) dx - sin(40^o) dy)

y koncový = y počiatočný + 0.7 (sin(40^o) dx + cos(40^o) dy)

Symbol - znamená otočiť sa doprava (použili sme prepis pre súradnice nového bodu

x koncový = x počiatočný + 0.7 (cos(33^o) dx + sin(33^o) dy)

y koncový = y počiatočný + 0.7 (sin(33^o) dx - cos(33^o) dy)

Vytvorte obrázok trojrozmerného stromčeka, kde jednotlivé vetvy sa nebudú skracovať faktorom 0.7, ale náhodným číslom s gaussovským rozložením pravdepodobnosti so stredom napr. v 0.7, kde aj hrúbka kmeňa sa bude zmenšovať a bližšie vetvy budú vyzerať hrubšie, kde uhly vetiev v priestore tiež budú dané náhodne. Vyskúšajte aj iné produkčné systémy, napr. počet vetiev bude daný náhodným číslom od 2 do 3.

(tému vypracuje Richard Bartelt, Richard.Bartelt@st.fmph.uniba.sk) (ps.zip pdf , dokumentacia projektu zip)

Téma 12. Namodelujte priebehy množstva dravcov a koristi ukázané v nasledujúcich obrázkoch podľa rovníc

dN₁(t)/dt = N₁(r_1- b₁N₂ )

dN₂(t)/dt = N₂(- r₂+b₂N₁

kde N₁(t) je počet kusov koristi (alebo hostiteľa) a N₂(t) je počet kusov dravcov (alebo parazitov) v čase t. Predpokladáme, že za neprítomnosti dravcov sa korisť rozmnožuje rýchlosťou r₁, zatiaľ čo za absencie koristi dravci hynú rýchlosťou r₂. Nech b₁ zodpovedá schopnosti dravcov požierať korisť a b₂ vplyvu množstva koristi (a teda nasýtenia dravcov) na ich rozmnožovanie. Nech r₁= 1.5, b₁=0.1 r₂= 0.25 b₂= 0.01 a N₁(0)= 15 a N₂(0)=20. Znázornite priebeh, nie však pomocou klasického riešenia pomocou diferenciálnych rovníc, ale vytvorením stochastického modelu, kde množstvá dravcov a koristi a ich prírastky/úbytky budú dané celými číslami; v prípade, že zmena nie je vyjadrená celým číslom, berte neceločíselnú časť ako pravdepodobnosť a rozhodnite o zaokrúhlení nahor/nadol na základe porovnania tejto pravdepodobnosti s náhodným číslom z intervalu (0,1) – použite analógiu algoritmov 10.1 a 10.2 z kapitoly o umelom živote. Numericky modelujte a diskutujte pravdepodobnosť zániku jedného či obidvoch druhov v závislosti na počiatočných množstvách jedincov a na ostatných parametroch.

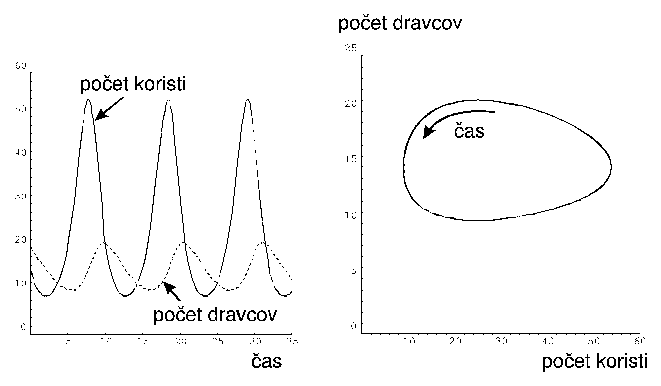
Prvá závislosť ukazuje oscilácie počtu dravcov a množstva koristi v čase, druhý obrázok je trajektóriou sústavy diferenciálnych rovníc (10.4).

(tému vypracuje Tomas Nalevajko, nalevajk@dcs.fmph.uniba.sk)

Téma 13. Vytvorte program pre animáciu pohybu žubrienok (pozri priložený obrázok), kde veľký kruh je prekážka, "hlavička žubrienok" predstavuje umiestnenie žubrienky v dvojrozmernom priestore a dĺžka a smer chvostíka určujú rýchlosť a smer pohybu žubrienky. Počítačový model sa má riadiť troma základnými vlastnosťami:

· vyhýbať sa kolízii s okolitými jedincami

· prispôsobiť rýchlosť okolitým jedincom

· snažiť sa držať sa blízko okolitých jedincov

Každá žubrienka pritom vidí iba svojich najbližších susedov. Pridajte "dravca", teda inofarebnú žubrienku, ktorá sa pohybuje smerom k ostatným žubrienkam a ktorej sa žubrienky snažia vyhýbať.

Zobrazenie ”žubrienok” (čiernych bodov s ”chvostíkom”), ktoré sa pohybujú smerom vpravo nahor a vyhýbajú sa prekážke (kruhu).

(tému vypracuje Ladislav Petrus, ladislav.petrus@rt.sk)

Téma 14. Standing Ovation. (Homework from Miching State University, see homepage http://zia.hss.cmu.edu/econ/homework95). Consider the following situation: Agents are seated in an auditorium listening to a brilliant economics lecture. At the end of the talk, after wiping away the tears, the applause begins, and perhaps a standing ovation ensues.

Model, using whatever techniques you desire, the process of a standing ovation.

• Explicitly state your model.
• Summarize any results.
• Suggest some potentially interesting future directions for the model.

Suggest some in nature appearing scenarios that could be usefully modeled using such a process.

(tému vypracuje Milada Kovárová, milada.kovarova@st.fmph.uniba.sk)

Téma 15. Použite simulované žíhanie pre riešenie pohybu koňa na šachovnici, kde zo zadaného poľa máte prebehnúť všetky ostatné poľa, pričom na každé pole vstúpite iba raz. Ako druhú časť úlohy riešte rovnaký problém s podmienkou, že sa kôň musí vrátiť naspäť. Pri riešení použite perturbáciu (mutáciu) toho druhu, že počiatok postupnosti polí do náhodne vybraného počtu polí skopírujete do nového riešenia a zvyšok vygenerujete. Úloha sa dá riešiť aj spätným prehľadávaním, ale len pre malé prípady.

(tému vypracuje Martin Lang, 9lang@pauli.fmph.uniba.sk)

Téma 16. (Bin Packing )

Pakovanie je klasickým problémom v optimalizácii. Predpokladajme, že máme nákladný voz schopný uviezť akýkoľvek počet krabíc, pokiaľ ich celková váha neprekročí W. V skladisku máte nelimitované množstvo rozličných typov tovaru. Každý typ položky i má váhu w_i a hodnotu v_i . Váš problém je určiť, ktorou kombináciou objektov dosiahnete najvyššiu hodnotu bez prekročenia maximálnej povolenej celkovej váhy. Napríklad, keď váhy a hodnoty sú

Položka	váha	hodnota
pomaranče	3	5
knihy	8	11

potom náklaďák s maximálnou nosnosťou W=200 môže viezť:

pomaranče	knihy	váha	hodnota
30	13	194	293
40	10	200	310
50	6	198	316
60	2	196	322

Najlepšia stratégia je naložiť toľko krabíc s pomarančmi ako sa len dá a zvyšok zaplniť knihami. Vyriešte problém pre väčší počet položiek s náhodne definovanými hodnotami a váhami pomocou genetického algoritmu, s obmedzeným počtom niektorých položiek, vymyslite si vlastnú reprezentáciu problému a k nej odpovedajúce chromozómy, mutácie a kríženie, porovnajte váš algoritmus s kanonickým genetickým algoritmom, a použite pokutovaciu funkciu. (Adaptované z http://www.epcc.ed.ac.uk/epic/ga/intro.html)

(tému vypracuje Michal Hitka, michal@hitka.sk)

Téma 17. Rozvrhovací problém (Scheduling problem)

Rozvrhovací problém je intenzívne v oblasti operačného výskumu už veľa rokov. Jednou z formulácií problému je predpokladať, že máme množinu N úkolov t_i, i=1..N, každý z nich vyžaduje niektoré zo zdrojov r_j po zadaný čas time_i,rj. Našou úlohou je nájsť najrýchlejší rozvrh pre celkové splnenie týchto úkolov, pričom zdroje môžu byť využívané súčasne, ale každý zdroj iným úkolom. Na poradí zdrojov pre úkol nezáleží. Vyriešte problém pre väčší počet úkolov s náhodne definovanými požadovanými zdrojmi a časmi pomocou genetického algoritmu, vymyslite si vlastnú reprezentáciu problému a k nej odpovedajúce chromozómy, mutácie a kríženie, porovnajte váš algoritmus s kanonickým genetickým algoritmom. Použite pokutovaciu funkciu pri nesplnení ohraničení.

(tému vypracuje Peter Rumpler, peter.rumpler@st.fmph.uniba.sk)

Téma 18. Evolúcia sortovacích sietí

(max. fitness = 120)

Vodorovné línie označujú pozície v sekvencii, vertikálne spoje dvoch horizontálnych línií reprezentujú operáciu výmeny zle usporiadanej dvojice (tzv. komparátor). Komparátor porovnáva dve čísla z pozícií určených horizontálnymi líniami, a keď sú zle usporiadané, prehodí ich. vzájomné pozície. Keď chceme vzostupnú sekvenciu a "horné" číslo je väčšia ako "dolné", prehodíme ich navzájom.

· Príklad: pre hodnoty 4,1,3,2 získaj 1,2,3,4 alebo 4,3,2,1 ako výstup: vertikálna čiara označuje výmenu hodnôt medzi horizontálnymi čiarami, keď je prvá hodnota väčšia/menšia ako tá druhá.

· Vyskúšaj: veľkosť populácie=10, kríženie=10%, mutácie=0%

· Vyskúšaj: veľkosť populácie =10, kríženie =10%, mutácie =1% (200 generácií)

· Vyskúšaj: veľkosť populácie =10, kríženie =80%, mutácie =1% (150 generácií)

· Vyskúšaj: veľkosť populácie =50, kríženie =90%, mutácie =1%

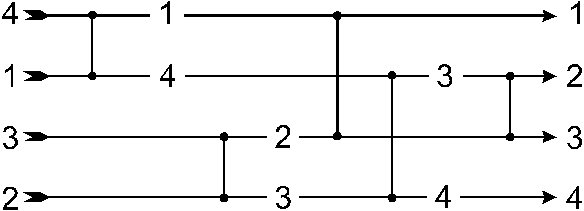
Príklad triediacej siete pre testovací príklad - sekvenciu (4,1,3,2), ktorá je korektne usporiadaná na sekvenciu (1,2,3,4). Táto sieť môže byť popísaná ako sekvencia komparátorov [1:2],[3:4],[1:3],[2:4],[2:3], kde čísla v zátvorkách sú indexy spojených línií, na ktorých výmena prebieha.

GA vytvára napr. pre prípad zoradenia piatich čísel 5-vstupové sortovacie siete obsahujúce najviac 9 porovnaní-výmen. Existuje 120 fitness prípadov (všetkých 5! permutácií sekvencie 1,2,3,4,5), a korektná sieť ich všetky zoradí bezchybne. Vyskúšaj koevolúciu pre zložitejšie prípady, kde sekvencie hodnôt sa vyvíjajú nezávisle a sú ohodnotené tým lepšie, čím viac sietí na nich zlyháva.

(tému vypracuje Peter Kozej, 9kozej@pauli.fmph.uniba.sk)

Téma 19. Genetické programovanie pre mravca hľadajúceho cestu

Genetickým programovaním vytvoriť "program" pre mravca pomocou súboru pravidiel. Mravec má zberať potravu rozsiatu na nie celkom súvislej dráhe umiestnenej na toroidálnej mriežke, pričom má iba obmedzené senzory (teda vidí iba na vedľajšie bunky mriežky). Mravec má za daný počet časových krokov zozberať čo najviac potravy. V detailoch zadania sa možno inšpirovať na

http://www2.informatik.uni-erlangen.de/~jacob/Evolvica/GP/Java/html/ant/ant.html).

Úlohou je vygenerovať pravidlá a) pre vlastnú náhodne vygenerovanú dráhu s podobnými vlastnosťami ako je John Muir Trail z vyše uvedenej WWW stránky. b) Vyskúšať vygenerovanie pravidiel, ktoré by platili pre viac dráh súčasne.

(tému vypracuje Tomáš Potok, potok@kopernik.cc.fmph.uniba.sk)

20. Simulované žíhanie pre kombinatorickú optimalizácia umiestenia prostriedkov

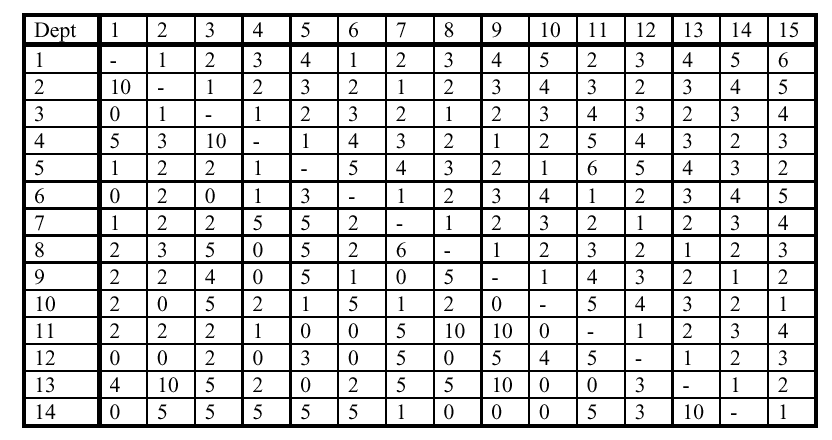
Tento problém QAP (quadratic assignment problem) podľa C.E. Nugent, T.E. Vollman, and J. Ruml, "An experimental comparison of techniques for the assignment of facilities to locations," Operations Research 16 (1968) pp. 150-173. 15 dielní má byť rozmiestnených do 15 pozícií. Cieľom je minimalizovať cenu transportu dodávok medzi rozmiestnenými oddeleniami. Cena transportu je (veľkosť dodávky * vzdialenosť), kde veľkosť dodávky aj vzdialenosť sú symetrické u ktorejkoľvek dvojice oddelení. V dolu uvedenej tabuľke je veľkosť dodávky medzi dieľňami (dolná polovina matice) a vzdialenosť možných umiestnení dieľní (horná polovina matice). Optimálne riešenie je 575 (alebo 1150 pre dvojnásobok tokov).

1. Urobte jednoduchý program na simulované žíhanie na riešenie problému. Na to potrebujete zakódovať problém, zadefinovať okolie (mutáciu), zvoliť postup znižovania teploty a ukončovacie kritérium.
2. Skúste porovnať výsledky tohto jednoduchého simulovaného žíhania s procesom prebiehajúcim na viac "procesoroch" na mriežke toroidu alebo na kružnici, keď s času na čas "procesory" akceptujú prípadné lepšie riešenie zo svojho okolia.

(tému vypracuje Ján Senko, JanoS@ksp.sk)

Vypracované "case studies" v šk.r. 2001/2002

 viď http://math.chtf.stuba.sk/evol/prednaska01.htm naspodku strany

Vypracované "case studies" v šk.r. 2000/2001

 viď http://math.chtf.stuba.sk/evol/prednaska00.htm naspodku strany

Vypracované "case studies" v šk.r. 1999/2000

 viď http://math.chtf.stuba.sk/evol/prednaska99.htm naspodku strany